A block of mass M with a semicircular track of radius R rests on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest from the top point A. The cylinder slips on the semicircular frictionless track. The distance traveled by the block when the cylinder reaches the point B is
Given that initially the system is at rest so vcm = 0. Now in slipping as no horizontal force is applied the horizontal component of velocity of centre of mass of the system must remain constant. So if v and V are the velocities of cylinder and block at B relative to the ground mv + MV/m+M = const. = 0 i.e. mv + MV = 0 as m + M = finite ...... 1 or m ∆r1/∆t+∆r2/∆t M=0 [as v = ∆r1/∆t] or mΔr1 + MΔr2 = 0 as Δr1 = d or md1 - Md2 = 0 as d2 is opposite to d1 ....... 2Now when the cylinder reaches from A and B it is displaced by a distance R - r horizontally to the right relative to the block. So if the displacement of the block relative to ground is d2 to the left the displacement of cylinder relative to ground to the right will be d1 = R-r - d2 ......3Substituting d1 from Equation 3 in2 we getM[R-r-d2]-md2 = 0i.e. d2 = mR-r/M+m to the left Therefore the distance traveled by the block when the cylinder reaches the point B isd2 = mR-r/M+m to the left
Related Solutions
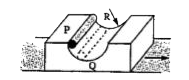
A block of mass M, with a semicircular track of radius R rest on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest at the point of the semicircular track. The cylinder slips in the semicircular frictionless track. How far the block moved when the cylinder reaches the bottom of the track ?
View SolutionA block of mass M with a semicircular track of radius R rests on a horizontal frictionless surface. A uniform cylinder of radius rand mass m is released from rest at top point P. The cylinder slips on the semicircular frictionless track. When cylinder reaches the bottom point Q, the distance moved by block is
View SolutionA block of mass M with a semicircualr of radius R, rests on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest the top point A The cylinder slips on the semicircular frictionless track. How far has the block moved when the cylinder reaches the bottom (point B) of the track ? How fast is the block moving when the cylinder reaches the bottom of the track?
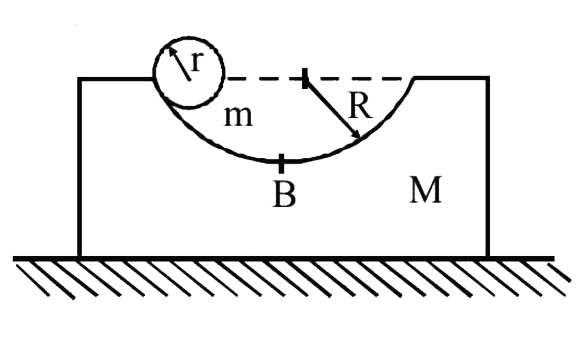
View SolutionA block of mass M with a semicircualr of radius R, rests on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest the top point A The cylinder slips on the semicircular frictionless track. How far has the block moved when the cylinder reaches the bottom (point B) of the track ? How fast is the block moving when the cylinder reaches the bottom of the track?
View SolutionA block of mass M with a semicircualr of radius R, rests on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest the top point A The cylinder slips on the semicircular frictionless track. How far has the block moved when the cylinder reaches the bottom (point B) of the track ? How fast is the block moving when the cylinder reaches the bottom of the track?
View SolutionA block of mass M with a semicircualr of radius R, rests on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest the top point A The cylinder slips on the semicircular frictionless track. How far has the block moved when the cylinder reaches the bottom (point B) of the track ? How fast is the block moving when the cylinder reaches the bottom of the track?
View SolutionA block of mass M with a semicircualr of radius R, rests on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest the top point A The cylinder slips on the semicircular frictionless track. How far has the block moved when the cylinder reaches the bottom (point B) of the track ? How fast is the block moving when the cylinder reaches the bottom of the track?

View SolutionA block of mass M = 2 kg with a semicircular track of radius R = 1.1 m rests on a horizontal frictionless surface. A uniform cylinder of radius r = 10 cm and mass = 1.0 kg is released from rest from the top point A. the cylinder slips on the semicircular frictionless track. The speed of the block when the cylinder reaches the bottom of the track at B is
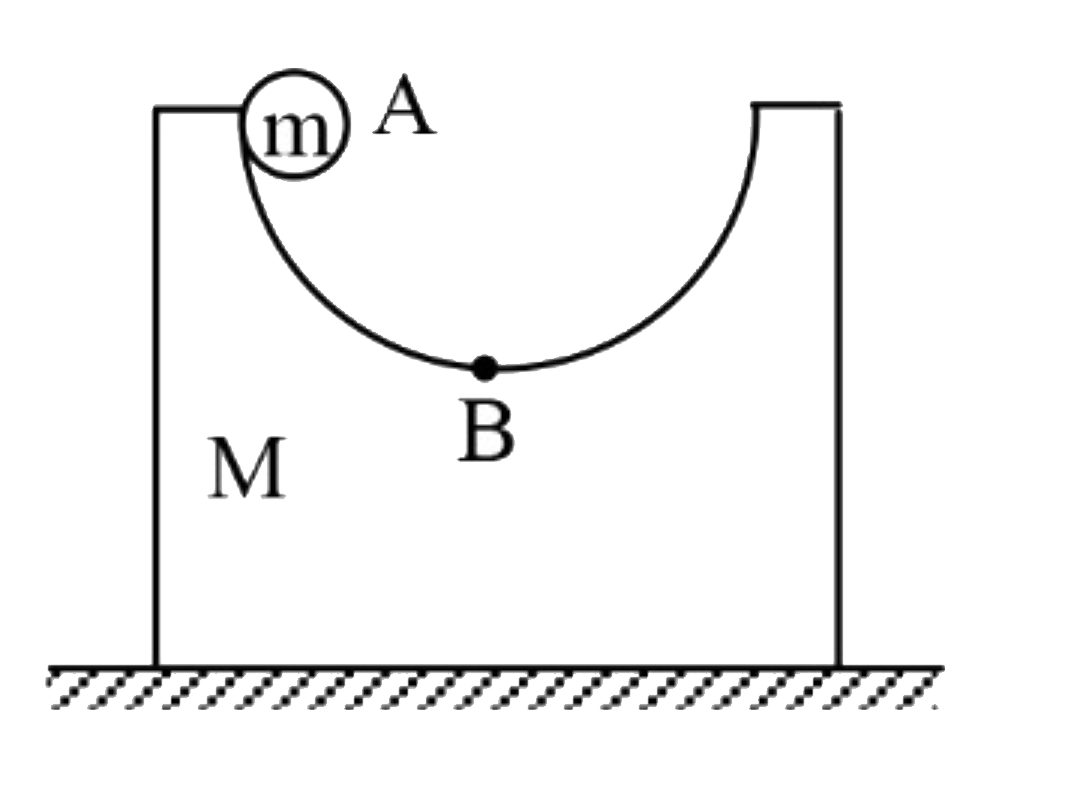
View SolutionA block of mass M = 2 kg with a semicircular track of radius R = 1.1 m rests on a horizontal frictionless surface. A uniform cylinder of radius r = 10 cm and mass = 1.0 kg is released from rest from the top point A. the cylinder slips on the semicircular frictionless track. The speed of the block when the cylinder reaches the bottom of the track at B is

View SolutionA block of mass M=2 kg is kept at rest along a semicircular track of radius R=1.1m on a horizontal frictionless surface. A uniform cylinder of radius r = 10 cm and mass m = 1.0 kg is released from rest from the top point A. The cylinder slides on a semicircular frictionless track. The speed of the block when the cylinder reaches the lowest B of the track. (g= 10m/s) s^(2) )
View SolutionA block of mass M with a semi circular track of radius R, rests on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest at the top point A. The cylinder slips on the semicurcular frictionless track. How far has the block moved when the cylinder reaches the bottom of the track ? How fast is the block moving when the cylinder reaches the bottom of the track ?
View SolutionA block with a semicircular path of radius R = 1.1 m whose mass M = 2 kg is at rest on a frictionless horizontal surface. A uniform cylinder of radius r = 10 cm and mass m = 1.0 kg is released from rest from the top point A. The cylinder slips on a frictionless horizontal surface. When the cylinder reaches the bottom of the path at point B, then the speed of the block is: (g = 10 m s^(-2))
View SolutionA uniform solid cylinder of mass 2 kg and radius 0.2 m is released from rest at the top of a semicircular track of radius 0.7 m cut in a block of mass M = 3 kg as shown in Fig. The block is resting on a smooth horizontal surface and the cylinder rolls down without slipping. Based on the above information, answer the following questions: The speed of the point of contact of the cylinder with the block w.r.t. ground, when the cylinder reaches the bottom of the track is
View SolutionA uniform solid cylinder of mass 2 kg and radius 0.2 m is released from rest at the top of a semicircular track of radius 0.7 m cut in a block of mass M = 3 kg as shown in Fig. The block is resting on a smooth horizontal surface and the cylinder rolls down without slipping. Based on the above information, answer the following questions: The speed of the point of contact of the cylinder with the block w.r.t. ground, when the cylinder reaches the bottom of the track is
View SolutionM द्रव्यमान का एक ब्लॉक किसी घर्षण रहित क्षेतिज सतह पर R त्रिज्या के अर्द्धवृत्ताकार मार्ग पर स्थित है। एक सर्वत्रसम (Uniform) बेलन जिसकी त्रिज्या r व द्रव्यमान m है, उच्चतम बिन्दु A से विरामावस्था से छोड़ा जाता है।
बेलन अ्द्धवृत्ताकार घर्षण रहित मार्ग पर फिसलता है। बेलन के मार्ग के निम्नतम बिन्दु B तक पहुँचने पर ब्लॉक कितनी दूरी तय कर लेगा? बेलन के मार्ग के निम्नतम बिन्दु तक पहुँचने तक ब्लॉक की गति क्या होगी?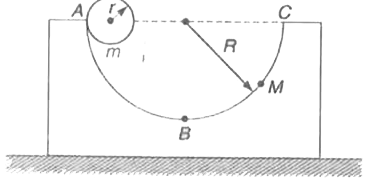
View SolutionA uniform solid cylinder of mass and radius is released from rest at the top of a semicircular track of radius cut in a block of mass as shown in Fig. The block is resting on a smooth horizontal surface and the cylinder rolls down without slipping. Based on the above information, answer the following questions:

The distance moved by the block when the cylinder reaches the bottom of the track is
View SolutionA uniform solid cylinder of mass and radius is released from rest at the top of a semicircular track of radius cut in a block of mass as shown in Fig. The block is resting on a smooth horizontal surface and the cylinder rolls down without slipping. Based on the above information, answer the following questions:

The distance moved by the block when the cylinder reaches the bottom of the track is
View SolutionA semicircular track of radius R=62.5cm is cut in a block. Mass of block having track, is M=1kg and rests over a smooth horizontal floor. A cylinder of radius r=10 cm and mass m=0.5kg is hanging by thread such that axes of cylinder and track are in same level and surface of cylinder is in contact with the track as shown in figure When the thread is burnt, cylinder starts to move down the track. Sufficient friction exists between surface of cylinder and track, so that cylinder does not slip. Calculate velocity of the block when it reaches bottom of the track. Also find force applied by block on the floor at that moment. (g=10m//s^(2))
View SolutionA semicircular track of radius R=62.5cm is cut in a block. Mass of block having track, is M=1kg and rests over a smooth horizontal floor. A cylinder of radius r=10 cm and mass m=0.5kg is hanging by thread such that axes of cylinder and track are in same level and surface of cylinder is in contact with the track as shown in figure When the thread is burnt, cylinder starts to move down the track. Sufficient friction exists between surface of cylinder and track, so that cylinder does not slip. Calculate velocity of the block when it reaches bottom of the track. Also find force applied by block on the floor at that moment. (g=10m//s^(2))
View SolutionA uniform solid cylinder of mass 2 kg and radius 0.2 m is released from rest at the top of a semicircular track of radius 0.7 m cut in a block of mass M = 3 kg as shown in Fig. The block is resting on a smooth horizontal surface and the cylinder rolls down without slipping. Based on the above information, answer the following questions: The speed of the cylinder when it reaches the bottom of the track is
View Solution