A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Fig. 4.28? What is the force on each case? Which case corresponds to stable equilibrium?
Magnetic field strength B = 3000 G = 3000 × 10−4 T = 0.3 TLength of the rectangular loop l = 10 cmWidth of the rectangular loop b = 5 cmArea of the loop A = l × b = 10 × 5 = 50 cm2 = 50 × 10−4 m2Current in the loop I = 12 ANow taking the anti-clockwise direction of the current as positive and vise-versa:a Torque From the given figure it can be observed that A is normal to the y-z plane and B is directed along the z-axis.The torque is1.8x10-2 N m along the negative y-direction. The force on the loop is zero because the angle between A and B is zero.b This case is similar to case a. Hence the answer is the same as a.c Torque From the given figure it can be observed that A is normal to the x-z plane and B is directed along the z-axis.The torque is1.8x10-2 N m along the negative x direction and the force is zero.d Magnitude of torque is given as:The torque is 1.8x10-2 N m at an angle of 240° with positive x direction. The force is zero.Hence the torque is zero. The force is also zero.Hence the torque is zero. The force is also zero.In case e the direction of lA and Bis the same and the angle between them is zero. If displaced they come back to an equilibrium. Hence its equilibrium is stable.Whereas in case f the direction of l vectorA and vectorB is opposite. The angle between them is 180°. If disturbed it does not come back to its original position. Hence its equilibrium is unstable.
Related Solutions
A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Fig. 4.28? What is the force on each case? Which case corresponds to stable equilibrium?
View SolutionA uniform magnetic field of 0.3 T is established along the positive Z-direction. A rectangular loop in XY plane of sides 10 cm and 5 cm carries a current of I = 12 A as shown. The torque on the loop is _____

View SolutionA unform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A . What is the torque on the loop in the different cases shown in the fig ? What is the force on each case? Which case corresponds to stable equilibrium ?
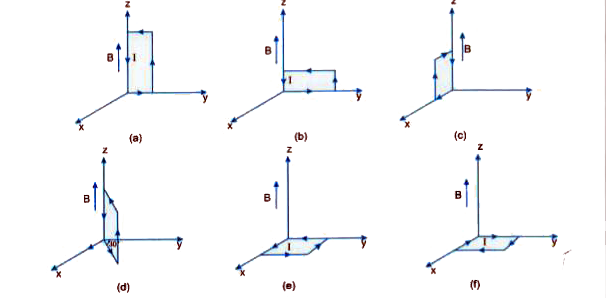
View SolutionA uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Figure? What is the force on each case? Which case corresponds to stable equilibrium?
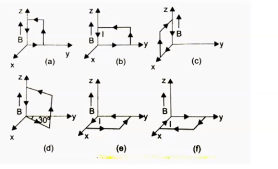
View SolutionA uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop shown in Fig. 4.28? What is the force? Is case corresponds to stable equilibrium? :
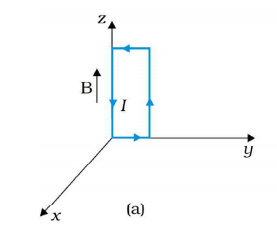
View SolutionA uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop shown in Fig. 4.28? What is the force ? is case corresponds to stable equilibrium? :
View SolutionA uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop shown in Fig. 4.28? What is the force ?is case corresponds to stable equilibrium? :
View SolutionA uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop shown in Fig. 4.28? What is the force ? is case corresponds to stable equilibrium? :
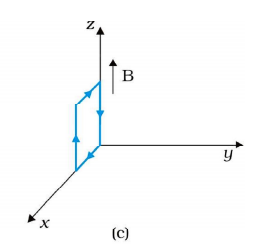
View SolutionA uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop shown in Fig.? What is the force ? is case corresponds to stable equilibrium? :
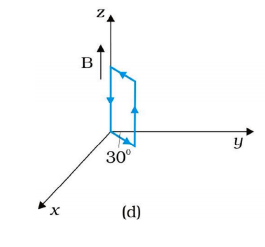
View SolutionA uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop shown in fig.? What is the force ? is case corresponds to stable equilibrium? :
View SolutionA uniform magnetic field of 3000G is established along the positive z-direction. A rect angular loop of sides 10 cm and 5 cm carries a current of 12A. What is the torque on the loop in different cases shown in the figure? What is the force on each case? Which case corresponds to stable equilibrium?
View SolutionA uniform magnetic field of 3000G is established along the positive z-direction. A rectangular loop of sides 10cm and 5cm carries a current 12A . What is the torque on the loop in the different cases shown in the figure. What is the force on each case? Which case corresponds to stable equilibrium?
View SolutionA uniform magnetic field of 3000G is established along the positive z-direction. A rectangular loop of sides 10cm and 5cm carries a current 12A . What is the torque on the loop in the different cases shown in the figure. What is the force on each case? Which case corresponds to stable equilibrium?
View SolutionA uniform magnetic field of 1000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop as shown in the figure?
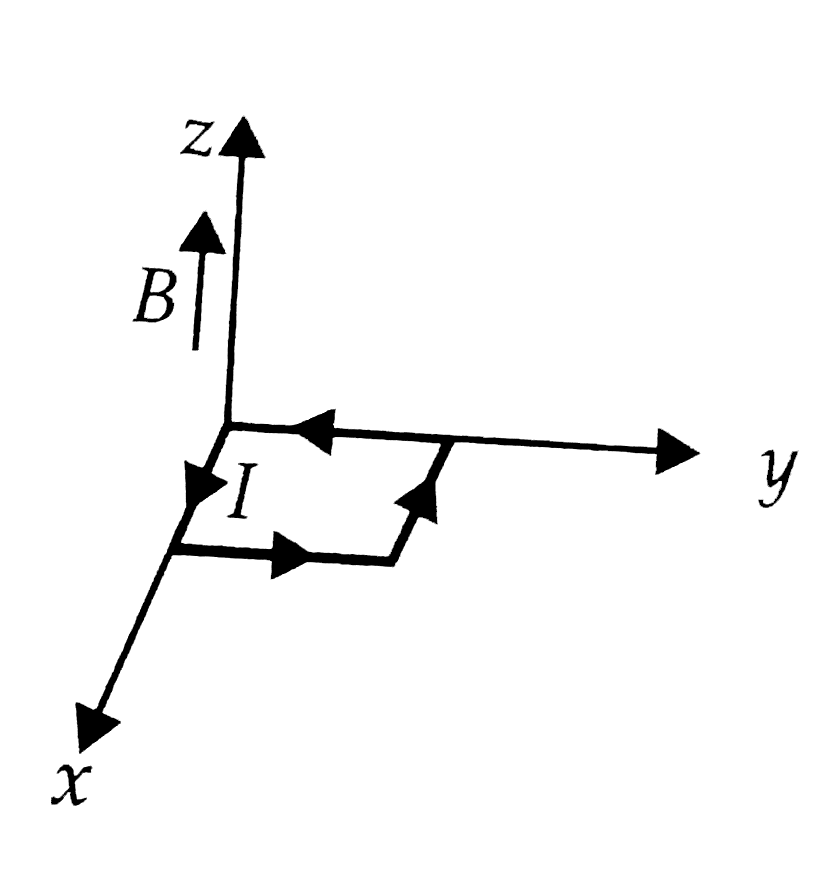
View SolutionA uniform magnetic field of 1000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop as shown in the figure?

View SolutionA uniform magnetic field of 1000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop as shown in the figure?
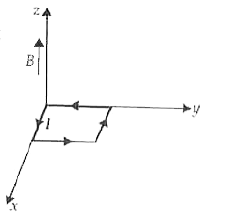
View SolutionA uniform magnetic field of 0.3 T is established along the positive Z-direction. A rectangular loop in XY plane of sides 10 cm and 5 cm carries a current of I = 12 A as shown. The torque on the loop is _____

View SolutionA uniform magnetic field of 0.3 T is established along the positive Z-direction. A rectangular loop in XY- plane of sides 10 cm and 5 cm carries a current of I = 12A as shown. The torque on the loop is

View SolutionA uniform magnetic field of 3000G is established along the positive Z-direction. A rectangular loop of sides 10cm and 5cm carries a current of 12A. The torque on the loop in the two cases shown are

View SolutionA uniformi magnetic field of 3 T is established along the positive Z-direction. A rectangular loop in XY plane of sides 10 cm and 5 cm carries a current of 11 A as shown The torque on the loop is:
View Solution