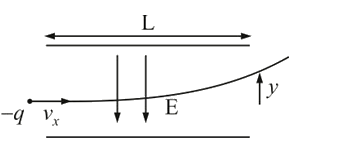
A particle of mass m and charge −q enters the region between the two charged plates initially moving along x-axis with speed vx like particle 1 in Figure. The length of plate is L and an uniform electric field E is maintained between the plates. Show that the vertical deflection of the particle at the far edge of the plate is qEL2/2mvx2.
Charge on a particle of mass m = − qVelocity of the particle =vxLength of the plates = LMagnitude of the uniform electric field between the plates = EMechanical force F = Mass m × Acceleration a⇒a=F/m⇒a=qE/m…………….1 [as electric force F = qE]Time taken by the particle to cross the field of length L is given by In the vertical direction initial velocity u = 0According to the third equation of motion vertical deflection s of the particle can be obtained as Hence vertical deflection of the particle at the far edge of the plate is qEL2/2mVx2. This is similar to the motion of horizontal projectiles under gravity.
Related Solutions
A particle of mass m and charge -q enters the region between the two charged plates initially moving along x-axis with speed as shown in figure. The length of plate is L and a uniform electric field E is maintained between the plates. The vertical deflection of the particle at the far edge of the plate is
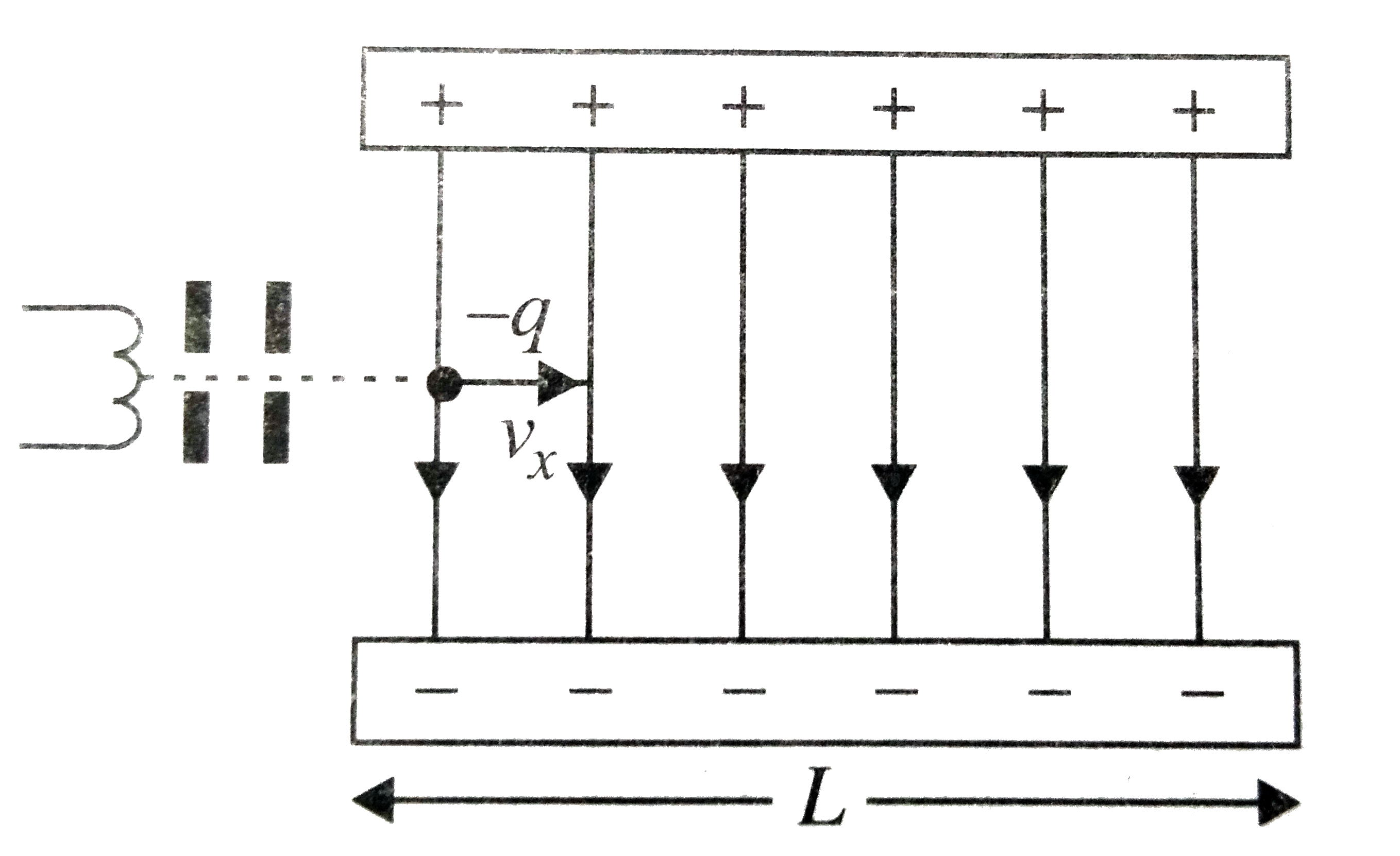
View SolutionA particle of mass m and charge (-q) enters the region between the two charged plates initially moving along x-axis with speed v_x. The length of plate is L and an uniform electric field E is maintained between the plates. Show that the vertical deflection of the particle at the far edge of the plate is .
View SolutionIn the above diagram, a particle of mass m and charge (- q) initially moving along X-axis with velocity v_x enters the region between two charged plates. The length of the plate system is L and uniform electric field between the plates is E. What is the vertical deflection of the particle at the far edge of the plate?
View SolutionA particle of mass m and change q enter the region between two charged plates. The length of the plate is L and there is a uniform electric field 'E' between those plates as shown. Charge q enters into the field with an initial speed U as shown. Find the vertical deflection of the particle at the far edge of the plate?
View SolutionA particle of mass m and charge (-q) enters the region between the two charged plates initially moving along x-axis with speed v_x (like particle 1 in figure. The length of plate is L and an uniform electric field E is maintained between the plates. Show that the vertical deflection of the particle at the far edge of the plate is qEL^(2)//(2m v_(x)^(2)) . Compare this motion with motion of a projectile in gravitational field discussed in Section 4.10 of Class XI Textbook of Physics.
View SolutionA particle of mass m and charge (-q) enters the regions between the two charged plates initially moving along x-axis with speed (like particle 1 in.) The length of plate is L and an the particle at the far edge of the plate is .
View SolutionA particle of mass m and charge enters the region between the two charged plates initially moving along X-axis with speed (like particle 1 in Fig.). The length of plate is L and a uniform electric field E is maintained
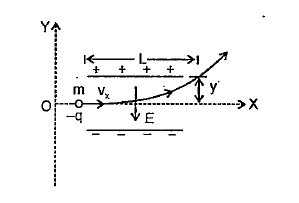
View SolutionA particle of mass m and charge (-q) enters the region between the two charged plates initially moving along x-axis with speed V_(x) (as in the fig.). The length of plate is L and an uniform electric field E is maintained between the plates. Show that the vertical deflection of the particle at the far edge of the plate is qEL^(2)//(2mV_(x)^(2)) . Compare this motion with motion of a projectille in gravitational field discussed in section 4.10 of 1^(st) Year Textbook of Physics.
View SolutionA particle of mass m and charge enters the region between the two charged plates initally moving along x axis with speed the length of plate is l and an uniform vertical deflectio of the particle at the far edge of the plate is
compare this motion with motion of a projectile in gravitational field
View Solutionद्रव्यमान m तथा आवेश (-q) का एक कण x-अक्ष के अनुदिश v चाल से गतिशील है। दो आवेशित प्लेटों के बीच से गुजरने के क्रम में इसका परवलीय पथ (parabolic path) चित्र में ABC द्वारा दिखाया गया है। यदि प्लेटो की लेबाई L तथा उनके बाच एकसमान विद्युत-क्षेत्र E हो, तो प्लेट के किनारे से निकलते समय तक कण का ऊर्ध्वाधर विक्षेप (vertical deflection) ज्ञात करें।
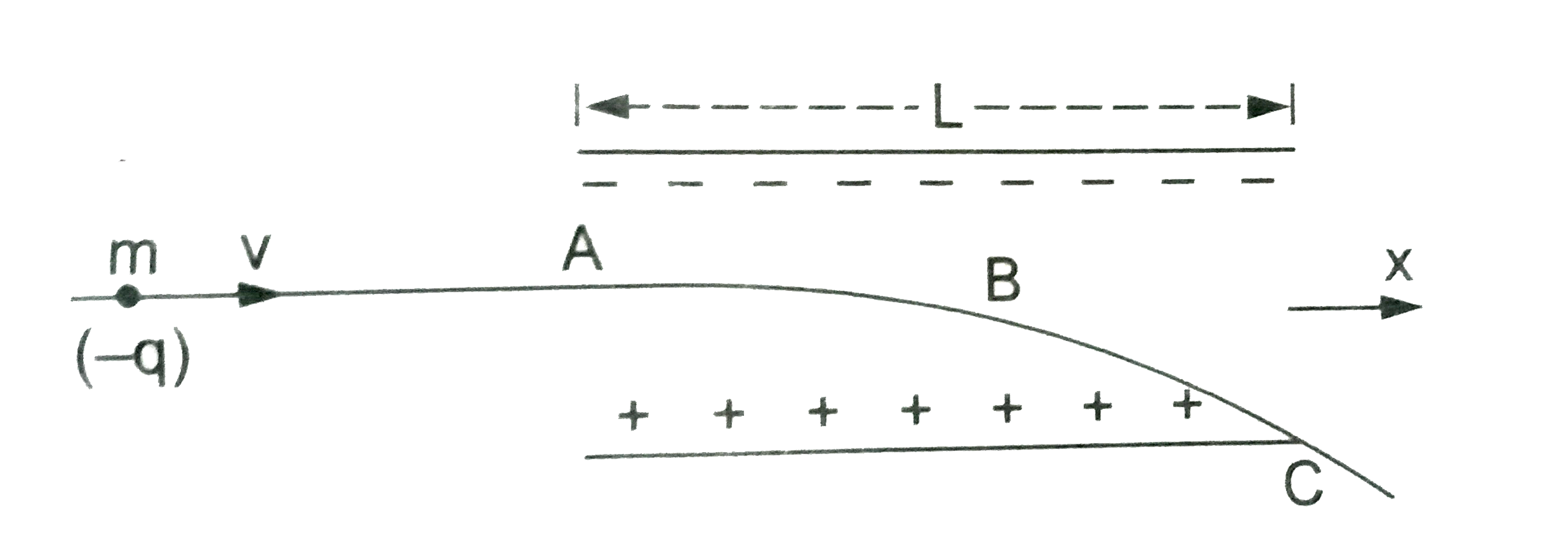
View SolutionA particle of mass m and charge enters the region between the two charged plates initally moving along x axis with speed v_(x) the length of plate is l and an uniform electric field E is maintained between the plates. Show that the vertical deflection of the particle at the far edge of the plate is qEL^(2)//2mv_(x)^(2) compare this motion with motion of a projectile in gravitational field
View SolutionA paraticale of mass m and charge enters the region between the two charged plates initially moving along x-axis with speed . The length of plate is L and a uniform electric field E is maintained between the plates. Show that the verticale deflection of the particle at the far edge of the plate is . Compare this motion with motion of a projectille in gravitional field.
View SolutionA particle of mass m and charge (-q) enters the region between the two charged plates initrally moving along X-axis with speed as shown in figure. The length of plate is L and an uniform electric field E is maintained between the plates. S.T. vertical deflection of the particle at the edge of the plate is .
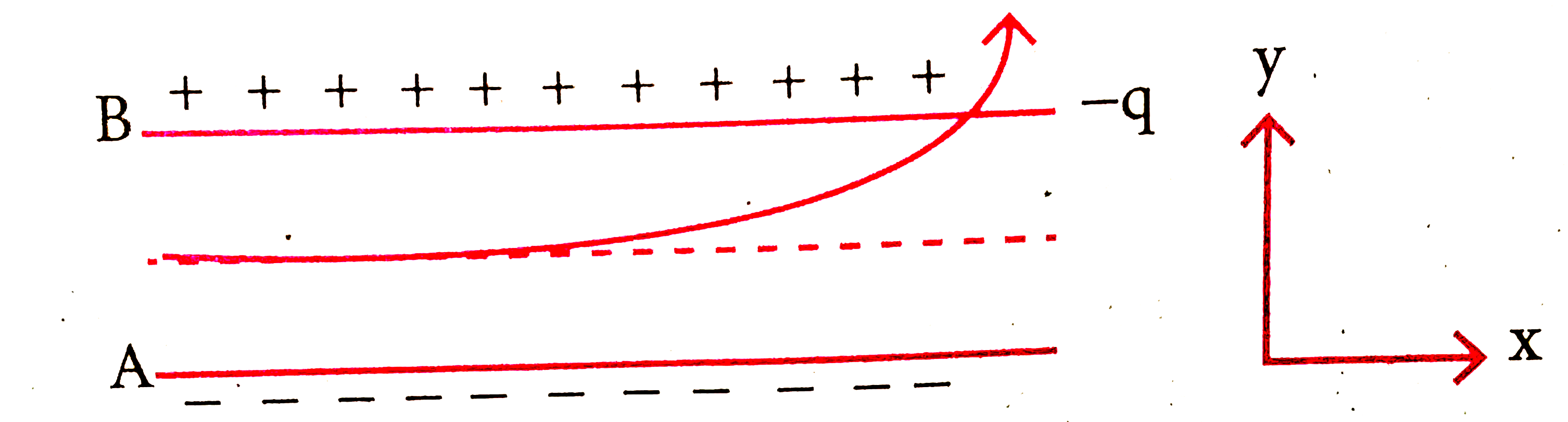
View SolutionA particle of mass m and charge(-q) enters the region between the two charged plates intially moving along x - axis with speed . The length of plate is L and a uniform electric field E is maintained between the plates . Show that the verticles deflection of the particle at the far edge of the palte is .
View SolutionIn the above diagram, a particle of mass"m" and charge(-q) initially moving along X-axis with velocity "v". The length of the plave system is "L" and uniform electric filed between the plates is "E". What is the vertical deflext of the particle at the far edge of the plate?
View Solutionप्रारम्भ में, x-अक्ष के अनुदिश चाल से गति करती हुए दो आवेशित प्लेटो के मध्य क्षेत्र में m द्रव्यमान तथा -q आवेश का कण प्रवेश करता है। प्लेटो की लम्बाई L है। इन दोनों प्लेटो के बीच एकसमान विधुत क्षेत्र E बनाए रखा जाता है। दर्शाइए की पटेल के अंतिम किनारे पर कण का उध्र्वाधर विक्षेप है।
View SolutionA uniform electric field of magnitude E exists in between two parallel metal plates , as shown in the figure given below. One particle of mass m and charge q is projected along the central line between the plates. Particle just missed to strike upper plate , while coming out of plates. Find : (a)Time taken by the particle to come out of plates. (b)Speed of the particle as it comes out of plates. (c) Angle of deviation suffered by particle. The length of the plates is L and the distance between the plates is d. Ignore gravity .
View SolutionBetween two horizontal parallel plates, uniform electric field directed vertically downward. A charged particle remains in equilibrium in vaccum between the plates. Find shortage/excess of electrons in the charged particle .
View Solutionm દળ અને (-q) વિદ્યુતભાર ધરાવતો એક કણ બે વિદ્યુતભારિત પ્લેટોની વચ્ચે વેગથી પ્રારંભમાં x-અક્ષને સમાંતરે દાખલ થાય છે (આકૃતિ 1.33માં કણ-1ની જેમ). દરેક પ્લેટની લંબાઈ L છે અને પ્લેટો વચ્ચે સમાન વિદ્યુતક્ષેત્ર જાળવી રાખવામાં આવે છે. દર્શાવો કે પ્લેટના દૂરના છેડે કણનું શિરોલંબ વિચલન છે. ધોરણ XI, ભૌતિકવિજ્ઞાન પાઠ્યપુસ્તકના પરિચ્છેદ 4.10માં ચર્સેલ પ્રક્ષિપ્ત પદાર્થની ગુરુત્વીય ક્ષેત્રમાંની ગતિ સાથે આ ગતિને સરખાવો.
View SolutionA uniform electric field vecE exists between the plates of a charged condenser. A charged particle enters the space between the plates and perpendiculars to vecE . The path of the particle between the plates is a
View Solution