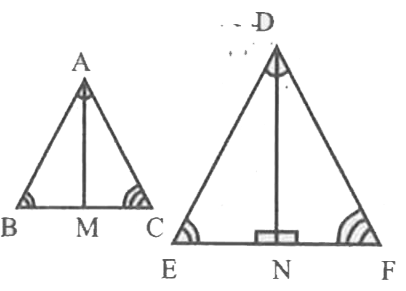
Areas of Similar Triangles:Prove that The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Proof: We are given two triangles ABC and PQR such that ΔABC ~ ΔPQRFor finding the areas of the two triangles we draw altitudes AM and PN of the triangles.
Related Solutions
The ratio of area of Two similar triangles is equal to the ratio of the squares of any two corresponding sides.
View SolutionThe ratio of areas of two similar triangles is equal to the ratio of the squares of corresponding…….
View SolutionTheorem 6.6 : The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
View SolutionTheorem 6.6 : The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
View SolutionThe ratio of the the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides/altitudes.
View SolutionThe ratio of the areas of two similar triangles is 1:4 then the ratio of their corresponding sides………….
View SolutionIf the ratio of areas of two similar triangles is 9:16 then the ratio of their corresponding sides is
View SolutionThe ratio of the corresponding sides of two similar triangles is 5:3. Then the ratio of their areas………..
View SolutionThe ratio of the areas of two similar triangles is , then ratio of their corresponding sides is :
View SolutionThe ratio of the area of two similar triangle is , the ratio of their corresponding sides are :
View SolutionArea of two similar triangles are in the ratio of 5:3 then the ratio of their corresponding sides is :
View SolutionAreas of two similar triangle are in the ratio of 5:3, then the ratio of their corresponding sides is :
View SolutionArea OF similar triangles || Ratio OF the area OF two similar triangles is equal to the square OF the ratio OF their corrosponding Side/Angle bisector/Median/Altitude|| Discussion OF ex.-6.5
View SolutionIf two triangles are similar; prove that the ratio of corresponding area is equal to the ratio of squares corresponding altitudes.
View SolutionProve that " the ratio of areas of two similar triangles is equal to the square of the ratio of their altitudes.
View SolutionFill in the gap :
The ratio of the areas of two similar triangles is equal to the square of the ratio of their _______.
View Solution