If a b c and d are in G.P. show that a2 + b2 + c2 b2 + c2 + d2 = ab + bc + cd2 .
Solution:a b c d are in G.P.Therefore bc = ad … 1b2 = ac … 2c2 = bd … 3It has to be proved that a2 + b2 + c2 b2 + c2 + d2 = ab + bc – cd2R.H.S.= ab + bc + cd2= ab + ad + cd2 [Using 1]= [ab + d a + c]2= a2b2 + 2abd a + c + d2 a + c2= a2b2 +2a2bd + 2acbd + d2a2 + 2ac + c2= a2b2 + 2a2c2 + 2b2c2 + d2a2 + 2d2b2 + d2c2 [Using 1 and 2]= a2b2 + a2c2 + a2c2 + b2c2 + b2c2 + d2a2 + d2b2 + d2b2 + d2c2= a2b2 + a2c2 + a2d2 + b2 × b2 + b2c2 + b2d2 + c2b2 + c2 × c2 + c2d2[Using 2 and 3 and rearranging terms]= a2b2 + c2 + d2 + b2 b2 + c2 + d2 + c2 b2+ c2 + d2= a2 + b2 + c2 b2 + c2 + d2= L.H.S.∴ L.H.S. = R.H.S.
Related Solutions
If the angles A,B,C of a triangle are in A.P.and sides a,b,c are in G.P. ,then a2,b2,c2 are in
View SolutionDiscussion OF Ex-9.4 (Optional)|| Important Result a2=b2+c2(PythagorasTheorem) ||Chapter summary
View Solutionসংখ্যারেখা তৈরি করে নীচের সংখ্যাগুলিকে সংখ্যারেখায় দেখাও ও নাম দাও। +5, -2, +3, -6, +2, -5, -এ যথাক্রমে A,B,C,D,E ও F নাম দাও। B থেকে E-এর দূরত্ব কত ঘর মেপে দেখো।
View SolutionMolecular Orbital Diagram Of B2, C2 ,N2 |S-P Mixing
View Solution35. If the sum of the roots of be equal to sum of the squares, then- (A) 2ac = ab + b2 (B) 2ab-bc + c2 c (D) None of these (D) None of these (C) 2bc -ac+2
View Solution0.जब C1 और C2 धरिता के संधारित समंतर क्रम में संयोगजीत किए जाते हैंपरिनामी धरिता है (A) C1+C2 (B) C1C2/(C1+C2) (C) (C1+C2)/C1C2 (D)C1/C2
View SolutionThe ratios a1/a2 , b1/b2 , c1/c2 Find out whether the given linear equations are pairwise compatible or incompatible: 2x - 3y = 8 and 4x - 6y = 9.
View SolutionIf the equation of the locus of a point equidistant from the points (a_1, b_1) and (a_2, b_2) is (a_1-a_2)x+(b_1-b_2)y+c=0 , then the value of c is a a2-a2 2+b1 2-b2 2 sqrt(a1 2+b1 2-a2 2-b2 2) 1/2(a1 2+a2 2+b1 2+b2 2) 1/2(a2 2+b2 2-a1 2-b1 2)
View SolutionIf the equation of the locus of a point equidistant from the points and is , then the value of is
View SolutionLet conditions C1 and C2 be defined as follows: C1: b^2- 4ac > 0, C2: a, -b, c are of same sign. The roots of ax^2+ bx + c = 0 are real and positive, if (a) both C1 and C2 are satisfied (b) only C2 is satisfied (c) only C1 is satisfied (d) None of these
View SolutionIf are unit coplanar vectors, then the scalar triple product is b. c. d.
View SolutionIf are unit coplanar vectors, then the scalar triple product is a. b. c. d.
View SolutionIf vec a , vec ba n d vec c are unit coplanar vectors, then the scalar triple product [2 vec a- vec b2 vec b- vec c2 vec c- vec a] is 0 b. 1 c. -sqrt(3) d. sqrt(3)
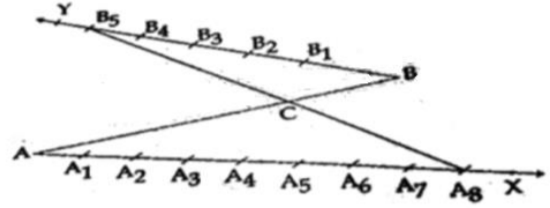
View SolutionIn the figure, if B1, B2, B3,…... and A1,A2, A3,….. have been marked at equal distances. In what ratio C divides AB?
View SolutionIf x = a cos θ and y = b sin θ, then b2x2 + a2y2 = …………… (1) a2b2 (2) ab (3) a4b4 (4) a2 + b2
View SolutionLet be a binary operation on the set Q of rational numbers as follows: find is it associative?
View SolutionA(a1, b1) மற்றும் B(a2, b2) ஆகிய புள்ளிகளை இணைக்கும் கோட்டுத் துண்டை X-அச்சு எந்த விகிதத்தில் பிரிக்கும்?
View SolutionLet be a binary operation on the set Q of rational numbers as follows: find is it commutative?
View SolutionIf a, b, c and d are in G.P., show that,
are in G.P.
View SolutionIf a,b,c,d are in G.P than show that ab,ca,bc,bd are also in G.P.
View Solution