When a plane wave front of light of wavelength 1 is incident on a narrow slit an intensity distribution pattern of the form shown is observed on a screen suitable kept behind the slit. Name the phenomenon observed.i Obtain the conditions for the formation of central maximum and secondary maxima and the minima. ii Why is there significant fall in intensity of the secondary maxima compared to the central maximum where as in double slit experiment all the bright fringes are of the same intensity ? iii When the width of the slit is made double the original width how is the size of the central band affected ?
The phenomenon observed is the phenomenon of diffractioni At the central maxima. The contribution due to the secondary wavelets from all parts of the wavefront at the slit arrive in phase at the central maxima θ = oAt the secondary maximaIt is only the contribution from nearly 1/3 or 1/5 or 1/7 ... of the secondary maxima. These occur at points for whichAt the minimaThe contribution from corresponding pairs of the sub-parts of the incident wavefront cancel each other and the net contribution at the location of the minima is zero. The minima occur at points for which ii There is a significant fall in intensity at the secondary maxima because the intensity there is only due to the contribution.n o{ nearly 1/3 or 1/5 or 1/7 .... of the incident wavefronts.iii The size of the central maxima would get halved when width of the slit is doubled.
Related Solutions
When a plane wave front of light, of wavelength , is incident on a narrow slit, an intensity distribution pattern, of the form shown is observed on a screen, suitably kept behind the slit. Name the phenomenon observed.
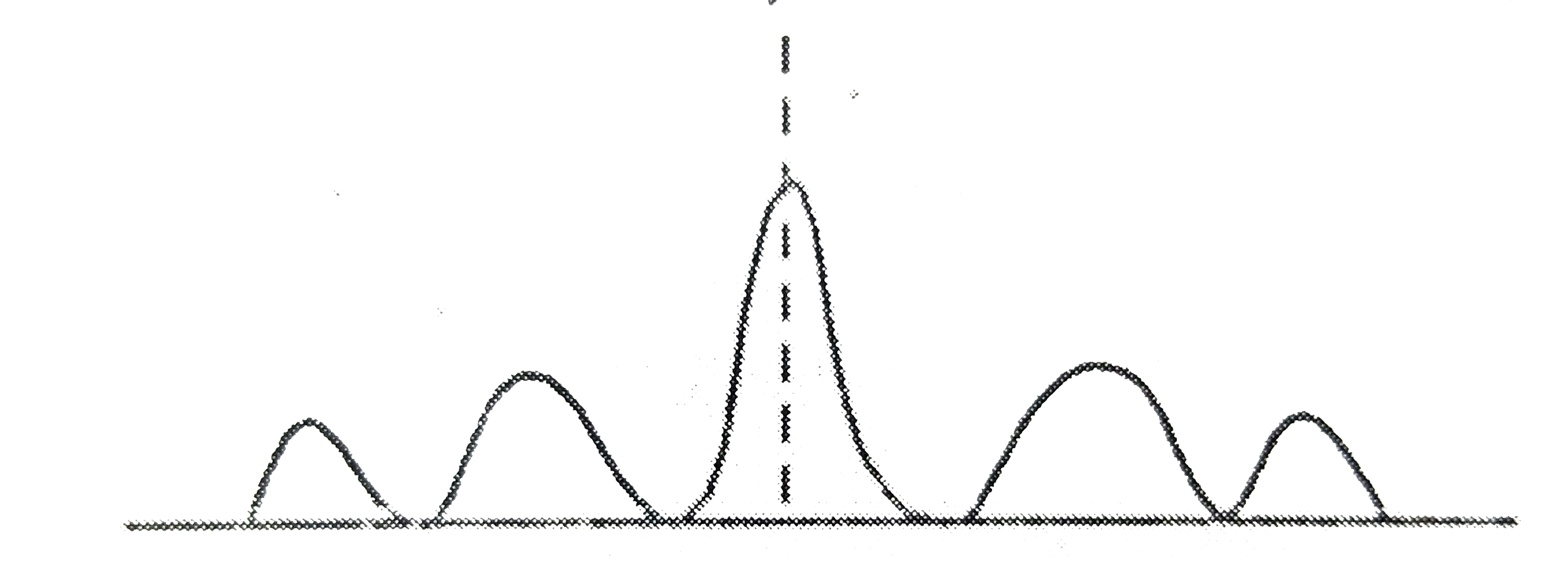
(a) Obtain the conditions for the formation of central maximum and secondary maxima and the minima.
(b) Why is there significant fall in intensity of the secondary maxima compared to the central maximum, whereas in double slit experiment all the bright fringes are of the same intensity ?
(c) When the width of the slit is made double the original width, how is the size of the central band affected ?
View SolutionFind the ratio of the intensities of the secondary maxima to the intensity of the central maximum for the single slit Fraunhofer diffraction pattern.
View SolutionFind the intensities of the first three secondary maxima in the single-slit diffraction pattern, measured relative to the intensity of the central maximum
View SolutionFind the ratio of the intensities of the secondary maxima to the intensity of the central maximum for the single slit Fraunhofer diffraction pattern.
View SolutionA monochromatic light of wavelength is incident normally on a narrow slit of width to produce a diffraction pattern on the screen placed at a distacne from the slit. With the help of a relevant diagram, deduce the condition for maxima and minima on the screen. use these condition to show that angular width of central maximum is twice the angular width of secondary maximum.
View SolutionIn a single-slit diffraction experiment, light of wavelength illuminates the slit of width 'a' and the diffraction pattern is observed on a screen.
(a) Show the intensity distribution in the pattern with the angular position .
(b) How are the intensity and angular width of central maxima affected when
(i) width of slit is increased, and
(ii) separation between slit and screen is decreased ?
View SolutionThe condition for obtaining secondary maxima in the diffraction pattern due to single slit is…
View SolutionThe condition for obtaining secondary maxima in the diffraction pattern due to single slit is
View SolutionThe condition for obtaining secondary maxima in the diffraction pattern due to single slit is
View SolutionThe ratio of light intensity at the maxima and minima in an interference pattern is 4:1. Find the ratio of intensity of light of two slits.
View SolutionWhat is diffraction of light? Explain the formation of maxima and minima due to diffraction from a rectangular narrow slit. Find the width of central maximum and also show that intensity of central maximum is inversely proportional to the width of the slit.
View SolutionIn a Young's slit experiment, the slit widths are in ratio 1:2. Determine the ratio of intensity of minima and maxima in the obtained interference pattern.
View SolutionA parralel beam of monochromatic light of wavelength 5000 Å is incident normally in a narrow slit of width 0.25 mm. The diffraction pattern is observed on a screen placed at a focal lens of a convex lens placed closed to the slit between slit and screen. Find the angular seperatiion between the first secondary maxima on either side of the central maximum.
View SolutionIn single slit diffraction pattern, why is intensity of secondary maximum less than the intensity of central maximum ?
View SolutionIn the Young's double slit experiment the central maxima is observed to be I_(0) . If one of the slits is covered, then intensity at the central maxima will become-
View SolutionIn the Young's double slit experiment, the central maxima is observed to be lo. If one of the slits is covered, then the intensity at the central maxima will become :
View SolutionIn the Young's double slit experiment the central maxima is observed to be I_(0) . If one of the slits is covered, then intensity at the central maxima will become-
View SolutionIn a YDSE using monochromatic visible light, the distance between the plate of slits and the screen is 1.7 m. At point P on the screen which is directly in front of the upper slit, maximum path is observed. Now, the screen is moved 50 cm closer to the plane of slits. Point P now lies between third and fouth minima above the central maxima and the intensity at P in one-fourth of the maxima intensity on the screen. ltbr> Find the wavelength of light if the separation of slits is 2 mm.
View SolutionIn a YDSE using monochromatic visible light, the distance between the plate of slits and the screen is 1.7 m. At point P on the screen which is directly in front of the upper slit, maximum path is observed. Now, the screen is moved 50 cm closer to the plane of slits. Point P now lies between third and fouth minima above the central maxima and the intensity at P in one-fourth of the maxima intensity on the screen. ltbr> Find the wavelength of light if the separation of slits is 2 mm.
View Solution(a) Describe briefly how a diffraction pattern is obtained on a screen due to a single narrow slit illuminated by a monochromatic source of light. Hence, obtain the conditions for the angular width of secondary maxima and secondary minima. (b) Two wavelengths of sodium light of 590 nm and 596 nm are used in turn to study the diffraction taking place at a single-slit of aperture 2xx10^(-6) m. the distance between the slit and the screen is 1.5m. calculate the separation between the positions of first maxima of the diffraction pattern obtained in the two cases.
View Solution