lf ω is an imaginary cube root of unity then 1 + ω - ω27 equal toa 128ωb - 128ωc 128ω2d - 128ω2
Correct option d - 128ω2Explanation:
Related Solutions
The value of (1−ω+ω^2 )^ 5 +(1+ω−ω^ 2 )^ 5 where ω and ω^ 2 are the complex cube roots of unity, is
View Solutioni) (1 + ω) (1 + ω ^ 4) (1 + ω ^ 8) = -ω ^ 2
View SolutionIf are connected in parallel, what will be the current through the resistor?
View SolutionIn the following circuit the equivalent resistance between A and B is
10 Ω
20 Ω
30 Ω
40 Ω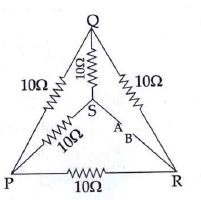
View Solutionइकाई के घन मूल #!# &
View SolutionIf omega is an imaginary cube root of unity.
View SolutionWhat is the effective resistance (in Ω) of two resistors 21 Ω and 28 Ω connected in parallel?
View SolutionIf a and b are imaginary cube roots of unity, then alpha^(n)+beta^(n) is equal to
View SolutionThe condition satisfied by the imaginary ,cube root of unity is
View SolutionProve the following
…. to 2n factors where , ω is the cube root of unity.
View Solutionis equal to (where is the imaginary cube root of unity and
View Solutionis equal to (where is the imaginary cube root of unity and
View SolutionWhen two resistors are connected to a circuit the resultant resistances are .Calculate the value of each resistor.
View SolutionIf is an imaginary cube root of unity, then is equal to
View SolutionIf w be imaginary cube root of unity then (1+w-w^(2))^(7) equals:
View SolutionIf is an imaginary cube root of unity, then equals :
View SolutionIf omega is an imaginary cube root of unity, then (1+omega-(omega)^2)^7 equals
View SolutionIf is an imaginary cube root of unity, then equals
View SolutionAn alternating current is given by 1 = 1 1 cos ω t + 1 2 sin ω t . sinomega t .The value of rms current is
View Solutionif 1,w,w^(2) be imaginary cube root of unity then the root of equation (x-1)^(3)+8=0 are :
View Solution