P is a point inside the triangle ABC. Lines are drawn through P parallel to the sides of the triangle. The three resulting triangles with the vertex at P have areas 4 9 and 49 sq. units. The area of the triangle ABC isA 2√3 B 12 C 24 D 144
D 1441 + 2 + 3 gives
Related Solutions
P is a point inside the triangle ABC. Lines are drawn through P, parallel to the sides of the triangle.The three resulting triangles with the vertex at P have areas . units. The area of the triangle ABC is -
View SolutionThree straight lines are drawn through a point P lying inside a triangle ABC, parallel to its sides. The area of the resulting triangles are 1,4 and 9 sq units. Find the area of in square units.
View SolutionPis a point inside the triangle ABC.Lines are drawn through P,parallel to the sides of the triangle.The three resulting triangles with the vertex at P have areas 4,9 and 49sq. units. The area of thetriangle ABC is -
View Solutionत्रिभुज ABC की भुजा BC का मध्य बिंदु D है तथा P उस पर कोई बिंदु है। PA के समांतर DE एक रेखा खेंची जाती है जो AC को E पर काटती है। यदि त्रिभुज ABC का क्षेत्रफल 12 वर्ग सेमी हो, तो त्रिभुज EPC का क्षेत्रफल ज्ञात करो।
View SolutionIf G is the centriod of and if area of is 5 sq units.Then area of is P sq units then value of P is
View SolutionTwo of the vertices of a triangle ABC and A (1,1) B-1,3) and the area of is 6 sq units. If P is the centroid of the , then find the locus of P.
View SolutionA triangle ABC is formed by three lines x+y+2=0,x-2y+5-0 and 7x+y-10=0. P is a point inside the triangle ABC such that areas of the triangles PAB,PBC and PCA are equal.If the co- ordinates of the point P are (a,b) and the area of the triangle ABC is delta, then find (a+b+delta).
View Solutiontriangle P is a point on BC in ABC such that BP:PC = 2 : 3 and point 9. is the mid point of BP, then ( triangle Area of ABQ : ( triangle The area of ABC) is equal to :
View SolutionLet be the vertices of a . If P is a point inside the triangle ABC such that the triangle APC,APB and BPC have equal areas, then length of the line segment PB is:
View SolutionLet be the vertices of a . If P is a point inside the triangle ABC such that the triangle APC,APB and BPC have equal areas, then length of the line segment PB is:
View SolutionSuppose P, Q and R are the mid-points of sides of a triangle of area 128 cm^2 . If a triangle ABC is drawn by joining the mid-points of sides of triangle PQR, then what is the area of triangle ABC?
View SolutionIn a triangle ABC, points P, Q and R are the mid-points of the sides AB, BC and CA respectively. If the area of the triangle ABC is 20 sq. units, find the area of the triangle PQR
View SolutionLet P, Q and R be 128 cm^2 are the mid-points of the sides of a triangle having area. if triangle PQR If a triangle ABC is formed by joining the mid-points of the sides of the triangle, then what will be the area of the triangle ABC?
View SolutionLet be a triangle of area 24sq. units and be the triangle formed by the mid-points of sides of Then the area of is 12 sq. units (b) 6 sq. units 4 sq. units (d) 3 sq. units
View SolutionLet be a triangle of area 24sq. units and be the triangle formed by the mid-points of sides of Then the area of is 12 sq. units (b) 6 sq. units 4 sq. units (d) 3 sq. units
View SolutionABC is a right triangle, right - angled at the vertex A. A circle is drawn to touch the sides AB and AC at points P and Q respectively such that the other end points of the diameters passing through P and Q lie on the side BC. IF AB = 6 units, then the area (in sq. units) of the circular sector which lies inside the triangle is
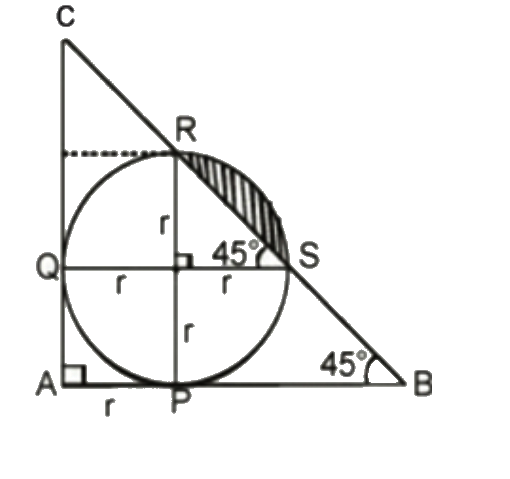
View SolutionABC is a right triangle, right - angled at the vertex A. A circle is drawn to touch the sides AB and AC at points P and Q respectively such that the other end points of the diameters passing through P and Q lie on the side BC. IF AB = 6 units, then the area (in sq. units) of the circular sector which lies inside the triangle is

View SolutionP is any point inside or on the boundary of having perimeter p and area R is any point in the plane of such that PR 5. the area of the region in which the point R lies is
View SolutionLet ABC be a triangle and P be a point inside ABC such that . The ratio of the area of triangle ABC to that of APC is - (A) (B) (C) (D)
View SolutionLet P be a point in the plane of such that the triangles PAB,PCA all have the same perimeter and the same area.
If P lies inside the then
View Solution