ln ΔABC the mid-points of sides BC CA and AB are D E and F respectively. Find ratio of ar ΔDEF to ar ΔABC.
In ΔABC Given that F E and D are the mid points of AB AC and BC respectively.Hence FE || BC DE || AB and DF || ACBy mid-point theorem.
Related Solutions
ΔDEF ~ ΔABC. If DE : AB = 2 : 3 and ar ΔDEF is equal to 44 square units then ar (ΔABC) (square unit) is
View SolutionD, E and F are respectively the mid-points of the sides AB, BC and CA of a ΔABC. Prove that by joining these mid-points D, E and F, the ΔABC is divided into four congruent triangles
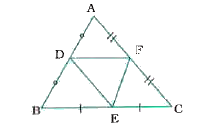
View SolutionIn the figure, ΔABC, D, E, F are the midpoints of sides BC, CA and AB respectively. Show that
(i) BDEF is a parallelogram
(ii)
(iii)
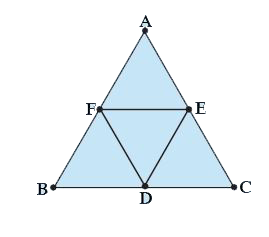
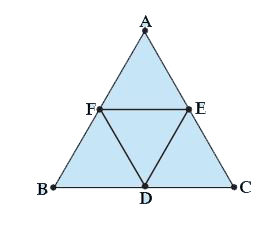
View SolutionIn the figure, ΔABC, D, E, F are the midpoints of sides BC, CA and AB respectively. Show that
(i) BDEF is a parallelogram
(ii)
(iii)
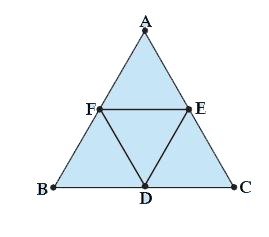
View SolutionIn the figure, ΔABC, D, E, F are the midpoints of sides BC, CA and AB respectively. Show that
(i) BDEF is a parallelogram
(ii)
(iii)
View SolutionIn ΔABC and ΔDEF AB = DE, BC = EF and BC // EF. Show that the vertices A, B and C are ,ABC≅ΔDEF which are connected to D, E and F respectively.
View SolutionD.E और F क्रमशः की भुजाओं के मध्य बिंदु है, तो = ?
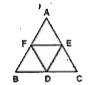
View Solutionऔर दो ऐसे त्रिभुज हैं कि
तो का मान होगा
View SolutionD, E and F are the mid-points of the sides BC, CA and AB of the triangle ABC respectively. show that ar (Delta DEF) = (1)/(4) ar (DeltaABC)
View SolutionD,E and F are mid-points of the sides BC, CA and AB respectively of triangleABC . Prove that ar(triangleDEF) = 1/4 ar (triangleABC)
View SolutionD,E and F are mid-points of the sides BC, CA and AB respectively of triangleABC . Prove that ar(||gmBDEF)= 1/2 ar (triangleABC)
View SolutionGiven that ΔABC∼ΔDEF,BC=3cm,EF=4cm ans the area of ΔABC is 54sq.cm.Then find the area of ΔDEF.
View SolutionΔABC ~ ΔDEF. If AB = 4 cm, BC = 3.5 cm, CA = 2.5 cm and DF = 7.5 cm, then the perimeter of ΔDEF is
View SolutionIn ΔABC and ΔDEF AB = DE, BC = EF and BC // EF. The vertices A, B and C are connected to D, E and F respectively AC = DF
View SolutionThe incircle of ΔABC touches the sides, AB, BC and AC in the point P, Q and R respectively. If AP=7cm, BC=13cm, find the perimeter of ΔABC.
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of a DeltaABC . Show that ar(triangleDEF)=1/4ar(triangleABC)
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of a DeltaABC . Show that ar(BDEF) = 1/2ar(triangleABC)
View SolutionABC is any triangle, D, E, F are the mid points of the sides respectively. Then are is
View SolutionD, E and F are respectively the mid-points of sides AB, BC and CA of . Find the ratio of the areas of .
View SolutionD, E and F are respectively the mid-points of sides AB. BC and CA of . Find the ratio of the areas of and .
View Solution