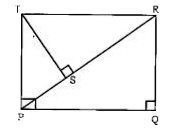
ΔPQR is right angled at Q. QX ⊥ PR XY ⊥ RQ and XZ ⊥ PQ are drawn. Prove that XZ2 = PZ x ZQ.
RQ ⊥ PQ XZ ⊥ PQor XZ || YQ.. Similarly XY || ZQXYQZ is a rectangle.
Related Solutions
In ,right-angled at Q,X,Y and Z are points on sides respectively such that . Find the value of XZ If .
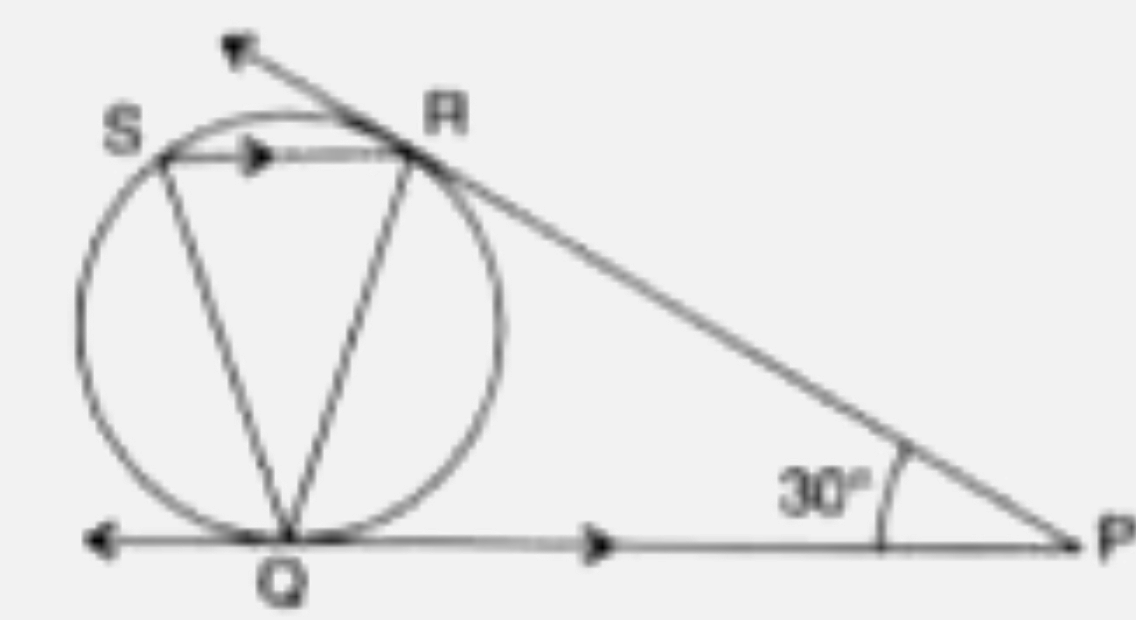
View SolutionIn the given figure, tangents PQ and PR are drawn to a circle such that angle RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the angle RQS.
View SolutionIf in triangles PQR and XYZ then :
View SolutionIf in triangles PQR and XYZ ; (PQ)/(XZ)=(PR)/(XY)=(QR)/(YZ) then:
View Solutionमें, PQ = PR भुजा PR एक बिंदु x इस प्रकार है कि सिद्ध कीजिए कि
View SolutionIf P, Q, R are 3 points on a line and Q lies between P and R, then prove that PQ=PR+RQ
View Solutionत्रिभुज PQR में यदि तो त्रिभुज का कौन-सा कोण समकोण होगा?
View SolutionIf then is equal to
View SolutionIf PQ be a diamter of a circle with centre at O and if PR= RQ, then the value of is
View SolutionIn the figure, RQPQ, PQPT and STPR. Prove that: ST QR = PS PQ
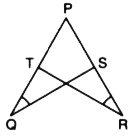
View SolutionDraw angles with the following given parts? a) I vertex, IJ and IK are the arms, b) X vertex, XZ and XY are the arms, c) Q vertex, PQ, RQ are the arms.
View SolutionIn the figure, PQ = PR and angle Q = angle R is. Prove that Delta PQS ~= Delta PRT is.
View SolutionThe given figure shows
Prove that
View SolutionTwo tangent lines PQ and PR are drawn on a circle such that angle PRQ = 30^(@) is. A chord RS tangent line is drawn parallel to PQ. angle RQS Find out
View SolutionPQR সমকোণী ত্রিভুজের সমকোণ এবং , RQ = 6 সেমি. হলে, PQ ও PR বাহুদ্বয়ের দৈর্ঘ্য হিসাব করে লেখো ।
View Solutionयदि P एवं Q, की भुजाओं XY एवं XZके मध्यबिन्दु हैं। PQ का मान होगा
View SolutionIf P and Q, Delta The arms of XYZ are the midpoints of XY and XZ. The value of PQ will be -
View SolutionDeltaPQR is a right angled at Q. If PQ=8cm and PR =(QR +2)cm . What is the value (in cm) of PR ?
View SolutionIn ,right angle is at Q,PQ =3cm and PR =6cm Determine
View SolutionIn ,right angle is at Q,PQ =3cm and PR =6cm Determine
View Solution