ABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain why O is equidistant from A B and C.
Since two right triangles make a rectangle where O is equidistant point from A B C and D because O is the mid-point of the two diagonals of a rectangle.Since AC and BD are equal diagonals and intersect at mid-point.So O is the equidistant from A B C and D.
Related Solutions
ABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you).
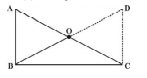
View SolutionABC is a a right angled triangle and O is the mid point of the side opposite to the right angle. Explain Why O is equidistant from A,B and C. (The dotted lines are drawn additionally to help you).

View SolutionABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you).

View SolutionABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain who O is equidistant from A,B and C. (The dotted lines are drawn additionally to help you.)
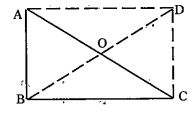
View Solution[ABC is a right-angled triangle and O is the mid point of the side opposite to the right angle.Explain why O is equidistant from A ,B and C .(The dotted lines are drawn additionally to help you).]
View Solution[ABC is a right-angled triangle and O is the mid point of the side opposite to the right angle.Explain why O is equidistant from A ,B and C .(The dotted lines are drawn additionally to help you).]
View SolutionABC एक समकोण त्रिभुज है और 'O' समकोण की सम्मुख भुजा का मध्य बिंदु है | बताइए कैसे 'O' बिंदु A, B तथा C से समान दूरी पर स्थित है | (बिंदुओं से चन्हित अतिरिक्त भुजाएँ आपकी सहायता के लिए खींची गई हैं )

View SolutionThe bisectors of angles ABC and BCA of a triangle ABC meet at point O. What is the angle at O opposite the side BC?
View SolutionIn Fig. 14.40, a right triangle is given. is the mid-point of the hypotenuse . Show that it is equidistant from the vertices and . (FIGURE)
View SolutionABC is a right angled triangle. B being the right angle. Mid-points of BC and AC are respectively B' and A'. Area of is
View SolutionThe side opposite to right angle in a right angled triangle-
View Solutionprove that right angles Delta AOB The mid-point of the hypotenuse in C is at equal distance to the vertices O, A and B of the triangle.
View SolutionABC एक समकोण त्रिभुज है और 'O' समकोण की सम्मुख भुजा का मध्य बिन्दु है। बताइये कैसे 'O' बिन्दु A, B तथा C से समान दूरी पर स्थित है। (बिन्दुओं से चिन्हित अतिरिक्त भुजाएँ आपकी सहायता के लिए खींची गई है)

View SolutionIn the given figure, find angle . If Angle is the right angle of triangle ABC and D is the mid point of side BC.
View Solutionएक ABC, C पर समकोणिक है। भुजाओं CA तथा CB पर क्रमश: P तथा Q मध्य बिन्दु हैं। ऐसे त्रिभुज में,
View Solutionएक AABC,C पर समकोणिक है। भुजाओं CA तथा CB पर क्रमशः P तथा Q मध्य-बिन्दु हैं। ऐसे त्रिभुज में,
View Solutionसमकोण त्रिभुज में समकोण के सामने की भुजा कहलाती है
View SolutionProve by vector method, that in a right-angled triangle ABC, , the angle A being right angled. Also prove that mid-point of the hypotenuse is equidistant from vertex.
View SolutionProve by vector method, that in a right-angled triangle ABC, , the angle A being right angled. Also prove that mid-point of the hypotenuse is equidistant from vertex.
View Solutionएक समकोण त्रिभुज ABC में कोण B समकोण है | यदि भुजाओ AB और BC पर क्रमश: बिंदु P और Q है, तो
View Solution