The angle of depression form the top of a tower of a point A on the ground is 30° . On moving a distance of 20 meters from the point A towards the foot of the tower to a point B the angle of elevation of the top of the tower to from the point B is 60° . Find the height of the tower and its distance from the point A.
So the height of the tower is 17. 32 m and its distance from the point A is 30 m.
Related Solutions
The angle of elevation of the top of a tower from a point A on the ground is . On moving a distance of 20 metres towards the foot of the tower to a point B, the angle of elevation increases to . Find the height of the tower and distance of the tower from the point A.
View Solutionएक मीनार के शीर्ष से सतह पर एक बिंदु A से उन्नयन कोण है|मीनार के पाद की ओर 20 मीटर चलने पर प्राप्त बिंदु B से यह उन्नयन कोण हो जाता है|मीनार की ऊंचाई तथा इसकी बिंदु A से दुरी ज्ञात कीजिए |
View SolutionThe angle of depression of a point A on the ground from the top of a tower 30^@ Is. The angle of elevation of the top of the tower from another point B at a distance of 20 m from point A to the foot of the tower 60^@ Is. Find the height of the tower and its distance from point A.
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is . If the height of the tower is 20m , find the distance of the point from the foot of the tower.
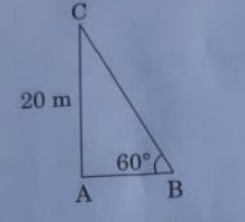
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is . If the height of the tower is 20m , find the distance of the point from the foot of the tower.
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is . If the height of the tower is 20m , find the distance of the point from the foot of the tower.
View SolutionThe angle of elevation of the to of a tower from a point A on the ground is . On moving a distance of 20 meters towards the foot of the tower to a point B, the angle of elevation increases to . What is the height of the tower ?
View SolutionFrom the top of a tower , which is 240m high , if the angle of depression of a point on the ground is . then the distance of the point from the foot of the tower is
View Solutionभूमि-तल पर स्थित एक बिन्दु A से एक मीनार के शीर्ष का उन्नयन कोण है | मीनार के पाद की तरफ 20 मीटर चलने पर एक दूसरे बिन्दु B से उन्नयन कोण बढ़कर हो जाता है|
(i)मीनार की ऊँचाई ज्ञात कीजिए |
(ii) बिन्दु A से मीनार की दूरी ज्ञात करें |
View Solutionएक मीनार के पाद से 40 मीटर दुरी पर स्तिथित किसी बिनु से मीनार के शिखर का उनयन कोण है मीनार की उचाई ज्ञात कीजिएः
View SolutionThe angle of elevation of the top of a tower of height 20 m from a point on the ground is 30^@ . Find the distance of point from foot of the tower.
View Solutionएक मीनार के आधार से 20 मीटर दूर भूमि पर स्थित एक बिंदु से मीनार की चोटी का उन्नयन कोण है|तब मीनार की ऊंचाई-
View SolutionThe angle of elevation of the top of a tower from a point at a distance of 100 m from the foot of the tower 30^(@) Is. The height of the tower is-
View SolutionThe angle of depression from the top of a tower 12m height, at a point on the ground is . The distance of the point from the tower is…………….
View SolutionFrom the top of a tower,the angle of depression of a point P on the ground is 30^(@) . If the distance of the point P from the tower be 24 meters then height of the tower is
View Solutionभूमि से किसी मीनार की ऊंचाई 20 मी० है,एक बिंदु से मीनार के शिखर का उन्नयन कोण है, मीनार की बिंदु से दूरी होगी -
View SolutionThe angle of elevation of the top of a tower at a point on the ground 20 m from the foot of the tower is . What is the height of the tower?
View SolutionFrom a point of the ground, angle of elevation of top of a tower is . On moving meter towards the tower the elevation changes to . What is the height of the tower ?
View SolutionFrom a point on the ground, which is at a distance of 30 m from the foot of a tower, the angle of elevation of the top of the tower is 30^@ Is. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower at a point on the ground, 50 m away from the foot of the tower, is 60°. Find the height of the tower.
View Solution