Given A = {Triangles} B = {Isosceles triangles} C = {Equilateral triangles}. State whether the following are true or false. Give reasons.i A ⊂ Bii B ⊆ Aiii C ⊆ Biv B ⊂ Av C ⊂ Avi C ⊆ B ⊆ A
A = {Tringles}B = {Isosceles triangles}C = {Equilateral triangles}
Related Solutions
Given, A = {Triangles}, B = {Isosceles triangles}, C = {Equilateral triangles}. State whether the following are true or false. Give reasons.
(i) , (ii) , (iii) , (iv) , (v) , (vi)
View SolutionWrite true/false of the following statements - The points (a,b,c,),(b,c,a) and (c,a,b) are the coordinates of the vertices of an equilateral triangle
View SolutionIn triangle ,where is the circumradius of the triangle. Then the triangle is
View SolutionIn triangle is the circumradius of the triangle. Then the triangle is a)isosceles but not right b)right but not isosceles c)right isosceles d)equilateral
View SolutionIn triangle A B C ,R(b+c)=asqrt(b c),w h e r eR is the circumradius of the triangle. Then the triangle is a)isosceles but not right b)right but not isosceles c)right isosceles d)equilateral
View SolutionA: In a , if A,B,C are in A.P. and triangle is equilateral cos A+2 cos B+ cos C=2
R: In a , if A,B,C are in A.P. and cos A+ cos B+ cos C=2 then the triangle is isosceles.
View SolutionCan an acute-angled triangled be a. and equilateral, b. an isosceles, and c. a scalene triangle ?
View SolutionIf A = {Equilateral triangles }, B = {Right angled triangles } and C = { Isosceles trian - gles } , then
View SolutionIn any triangle ABC if 2cos B=(a)/(c), then the triangle is(A) Right angled (C) Isosceles (B) Equilateral (D) None of these
View SolutionA(-4,0),B(4,0) and C(0,3) are the vertices of _-
a)an Equilateral triangle b)an Isosceles triangle c)a Right angled triangle d)a Scalane triangle
View SolutionIn a triangle a=2b and A=3B .Mention which of the following is true? A.) The triangle is equilateral B.) The triangle is isosceles C.) The triangle is right angled D.) The existence of such a triangle is not possible
View SolutionIf in a , prove that the triangle is isosceles.
View SolutionIn the figure, and . Prove that is an isosceles triangle.
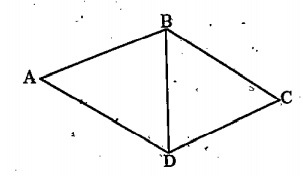
View Solutionयदि किसी त्रिभुज ABC में , तो दिखलाये कि त्रिभुज समद्विबाहु है |
View SolutionIn a triangle then the triangle is- right angled triangle (b) abtuse angled triangle acute angled triangle, which is not isosceles Equilateral triangle
View Solutionis an isosceles triangle with . If , prove that is right triangle.
View SolutionThe points (-a ,-b),(a , b),(a^2,a b) are (a) vertices of an equilateral triangle (b) vertices of a right angled triangle (c) vertices of an isosceles triangle (d) collinear
View SolutionThe points are (a) vertices of an equilateral triangle (b) vertices of a right angled triangle (c) vertices of an isosceles triangle (d) collinear
View SolutionThe points are (a) vertices of an equilateral triangle (b) vertices of a right angled triangle (c) vertices of an isosceles triangle (d) collinear
View SolutionIn an equilateral triangle if , then
View Solution