Draw an inscribing circle of a regular hexagon of side 5.8 cm.
Steps of Construction:i Draw a line segment AB = 5.8 cmii At A and B draw rays making an angle of 120o each and cut off AF = BC = 5.8 cmiii Again F and C draw rays making an angle of 120o each and cut off FE = CD = 5.8 cm.iv Join DE. Then ABCDEF is the regular hexagon.v Draw the bisectors of ∠A and ∠B intersecting each other at O.vi From O draw OL ⊥ ABvii With centre O and radius OL draw a circle which touches the sides of the hexagon.This is the required in circle of the hexagon.
Related Solutions
A regular hexagon & a regular dodecagon are inscribed in the same circle if the side of the dodecagon is then the side of the hexagon is
View SolutionDraw a circle circumscribing a regular hexagon with side 5 cm.
View SolutionWhat is the difference in the areas of the regular hexagon circumscribing a circle of radius 10 cm and the regular hexagon inscribed in the circle?
View Solution. Find the length of the side of a regular hexagon inscribed in a circle of radius r meters
View SolutionDraw a regular hexagon of side 5 cm.
View SolutionFind the difference in the area of a circle circumscribed about a regular hexagon with sides of 10cm and the area of the circle inscribed inside the same hexagon.
View SolutionConstruct a regular hexagon of side 4 cm. Construct a circle circumscribing the hexagon.
View SolutionA regular hexagon and regular dodecagon (12 sides) are inscribed in the same circle.If the side of the dodecagon is sqrt(3)-1. Then the side of the hexagon is:
View SolutionA regular hexagon is inscribed in a circle of radius 5 cm. If is the area inside the circle but outside the regular hexagon, then which one of the following is correct?
View SolutionIf a regular hexagon is inscribed in a circle of radius r, then find the perimeter of the hexagon.
View SolutionIf a regular hexagon is inscribed in a circle of radius 4 cm, then find the area of the polygon in cm^2
View SolutionA regular hexagon is inscribed in a circle of radius 14 cm. Find the area of the region between the circle and the hexagon.
View SolutionQ.4. Attempt any two of the following: (1) A regular hexagon is inscribed in a circle of radius 14 cm. Find the area of the region between the circle and the hexagon.
View SolutionA regular hexagon is inscirbed in a circle of radius R . Another circle is inscribed in the hexagon . Now another hexagon is inscribed in the second ( smaller ) circle .
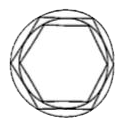
What is the ratio of area of inner circle to the outer circle ?
View SolutionA regular hexagon is inscirbed in a circle of radius R . Another circle is inscribed in the hexagon . Now another hexagon is inscribed in the second ( smaller ) circle .
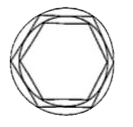
What is the sum of perimeters of both the hexagons ?
View SolutionIf a regular hexagon circumscribes a circle of radius r , then its perimeter is :
View SolutionIf a regular hexagon is inscribed in a circle of radius r , then its perimeter is :
View SolutionWhat is the area of a regular hexagon inscribed in a circle of radius r ?
View SolutionA regular hexagon is inscribed in a circle. What is the ratio of the area of the circle to that of its portion not covered by the hexagon?
View Solution