TA and TB are tangents to a circle with centre O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.
Join PB.In ΔTAP and ΔTBP TA = TB tangents segments from an external points are equal in lengthAlso ∠ATP = ∠BTP. since OT is equally inclined with TA and TB TP = TP commonΔTAP ≅ ΔTBP by SAS criterion of congruency∠TAP = ∠TBP corresponding parts of congruent triangles are equalBut ∠TBP = ∠BAP angles in alternate segmentsTherefore ∠TAP = ∠BAP.Hence AP bisects ∠TAB.
Related Solutions
TA and TB are tangents to a circle with centre O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.
View Solutionयदि दो वृत्त P बिंदु पर अंत: स्पर्श करते हो, एवं P से खींची गई स्पर्श रेखा पर T कोई बिंदु है जहाँ से दोनों वृत्तों पर TA और TB स्पर्श रेखाएं खींची जाए तो सिद्ध करें कि TA =TB|
View Solutionचित्र में, TA और TB एक बाह्रा बिन्दु T से वृत्त C (O, r) पर खींची गयी स्पर्श रेखाएँ हैं और रेखाखण्ड OT वृत्त को P पर प्रतिच्छेद करता हैं । सिद्ध कीजिए कि .
View Solutionयदि एक बिन्दु T से O केन्द्र वाले किसी वृत्त पर TA व TB स्पर्श रेखाएँ परस्पर के कोण पर झुकी हों, तो को ज्ञात कीजिए |
View SolutionT is a point on the common tangent at P to two circles and TA and TB are tangents to the other A respectively at A and B of two circles drawn from the point T, then
View SolutionT is a point on the common tangents at P of two circles and if TA and TB are respectively the other tangents at A and B to the two circles drawn from the point T then
View SolutionTA and TB are tangents to a circle from an external point T. If , then the is :
View SolutionProve that the length of the tangent drawn from an external point to a circle are equal. Using the above, do the following: TP and TQ are tangents from T to the circle with circle O and R in any point on the circle. If AB is a tangent to the circle at R, prove that TA + AR =TB +BR.

View SolutionTwo tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that .
View SolutionO is the centre of a circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find length of AB.
View SolutionO is the centre of a circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find length of AB.
View SolutionTwo radii OA and OB of a circle with centre O are perpendicular to each other. If two tangents are drawn at the point A and B intersect each other at the point T, prove that and they bisect each other at a ridght angle.
View Solutionबगल की आकृति में, TP तथा TQ स्पर्शरेखाऐं है जो हाहानबिंदु T से O केनदेवाले वृत पर खींची गई है तथा R वृत पर एक अन्य बिंदु है | यदि R पर की स्पर्शरेखा AB हो तो सिद्ध करें की TA + AR = TB + BR.
View SolutionAP and AQ are two tangents drawn from an external point A to a circle with centre O, P and Q are points of contact. If PR is a diameter, prove that
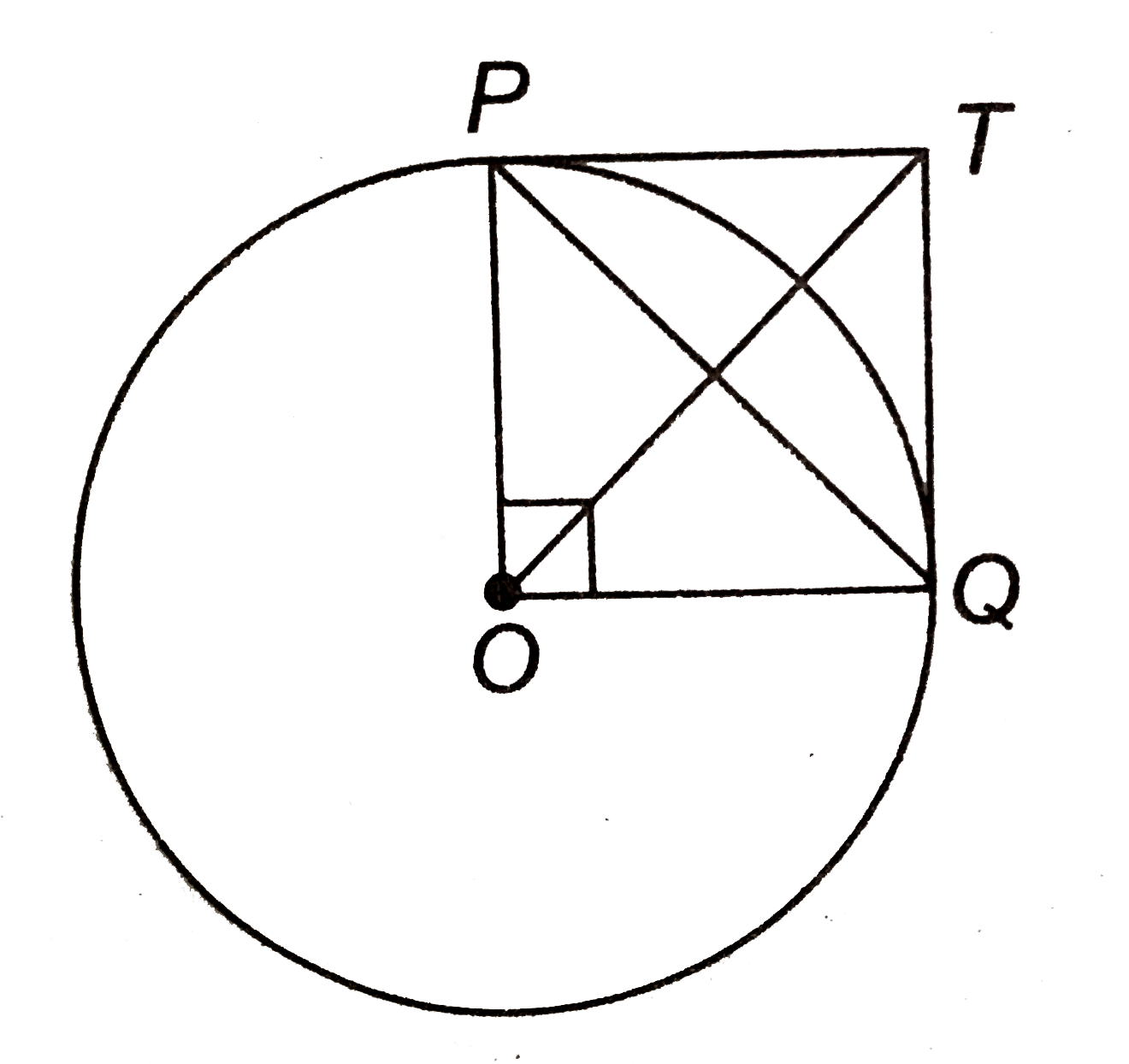
View SolutionIn the figure, The tangents to the circle with centre O at P and Q intersect at a point T. Prove that PQ and OT are right bisectors of each other.

View Solutionदी आकृति में, है। O केन्द्र के वृत्त में, बिन्दु P और Q पर खींची स्पर्श रेखायें बिन्दु T पर कटती है। सिद्ध कीजिए कि PQ और OT एक-दूसरे को समकोण पर समद्विभाजित करती है।
View SolutionThe length of the tangent from an external point P on a circle with centre O is
View SolutionO is the centre of a circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E, find the length AB.
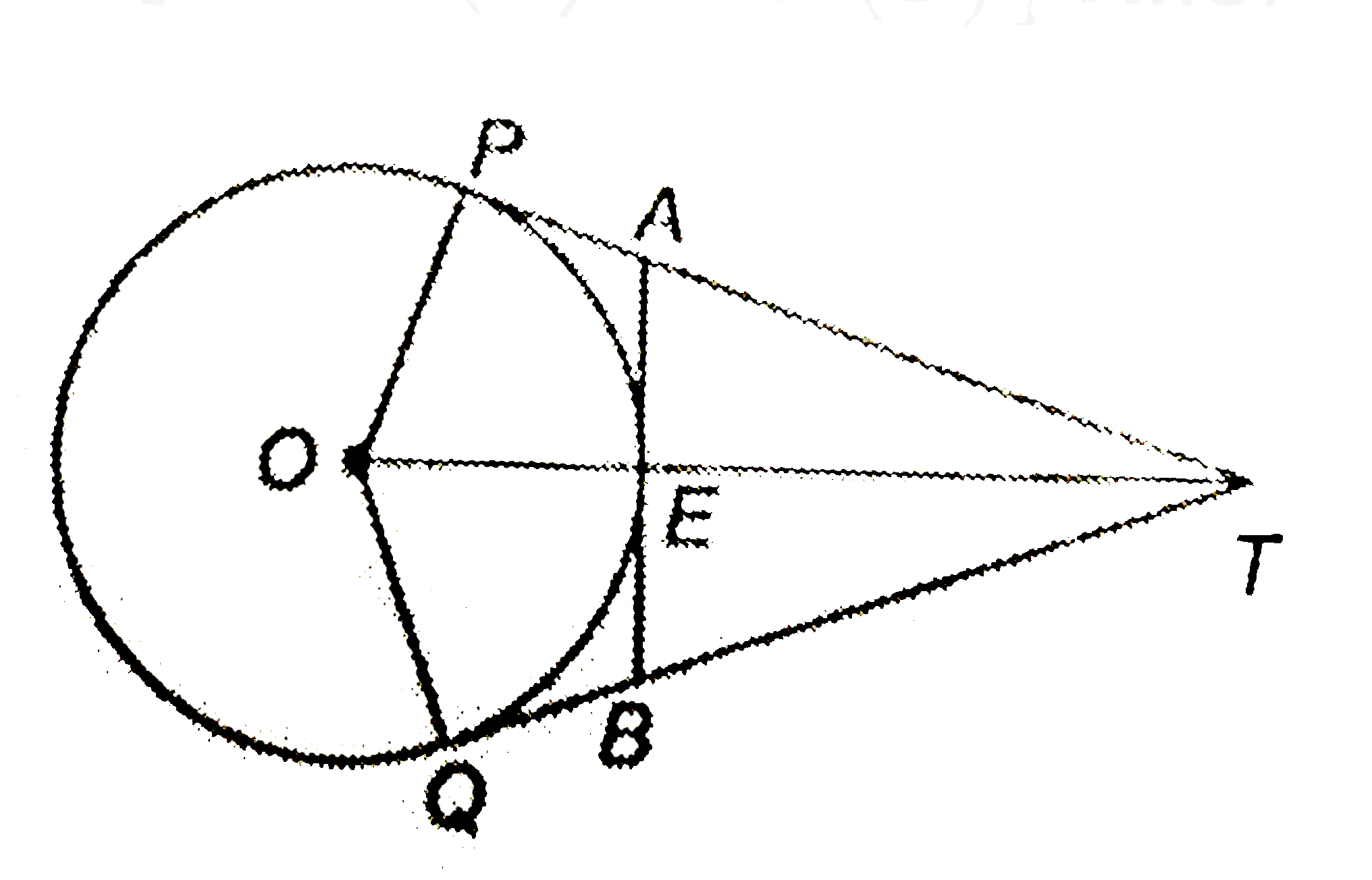
View SolutionO is the centre of a circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E, find the length AB.

View Solutionदो वृत्त परस्पर P बिंदु पर बाह्यतः स्पर्श करते हैं और उभयनिष्ठ स्पर्श रेखाएं उन्हें A और B पर स्पर्श करती हैं तो सिद्ध कीजिए (i) P से खींची गई उभयनिष्ठ स्पर्श रेखाएं AB को समद्विभाजित करती है|
(ii) रेखा AB बिंदु P पर समकोण अंतरित करती है।
View Solution