If two tangents are drawn to a circle from an external point show that they subtend equal angles at the centre.
Given: A circle with center O and a point A outside it. Also AP and AQ are the two tangents to the circle
Related Solutions
The tangents drawn from an external point to a circle (i) are equal, (ii) subtend equal angles at the centre.
View SolutionChoose the CORRECT option about the two tangents drawn to the circle from the external point? 1. The tangents subtend equal angles at the centre of the circle. 2. The tangents drawn from the external point to a circle are equal in length. 3. The tangents are equally inclined to the segment which joins the centre to that point.
View SolutionAssertion(A) If two tangents are drawn to a circle from an external point then they subtend equal angles at the centre.
Reason (R ) A parallelogram circumscribing a circle is a rhombus
View SolutionFrom an external point two tangents to a circle are drawn. The chord passing through the points of contact subtends an angle at the centre. The angle between the tangents is
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line - segment joining the points of contact at the centre.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
View SolutionProve that the angle between two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact at the centre.
View SolutionProve tht the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
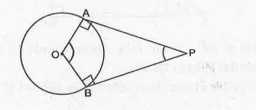
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line -segment joinig the point of contact at the centre.
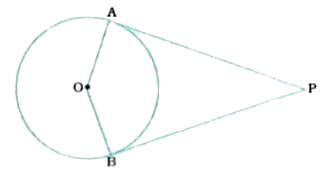
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
View SolutionProve that the angle between two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact at the centre.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact at the centre.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line - segment joining the points of contact at the centre.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line - segment joining the points of contact at the centre.
View Solution