In the following figure D and E are two points on BC such that BD = DE = EC. Show that ar ABD = ar ADE = ar AEC. Can you answer the question that you have left in the ’Introduction’ of this chapter whether the field of Budhia has been actually divided into three parts of equal area?[Remark: Note that by taking BD = DE = EC the triangle ABC is divided into three triangles ABD ADE and AEC of equal areas. In the same way by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC you can divide ΔABC into n triangles of equal areas.]
Let us draw a line segment AM ⊥ BC.We know that Area of a triangle = 1/2 x Base x AltitudeIt is given that DE = BD = EC.⊥ Area ΔADE = Area ΔABD = Area ΔAECIt can be observed that Budhia has divided her field into 3 equal parts.
Related Solutions
In, D and E are two points on BC such that BD = De = EC. Show that ar (ABD) = ar (ADE) = ar (AEC).
Can you now answer the question that you have left in the 'introduction' of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?
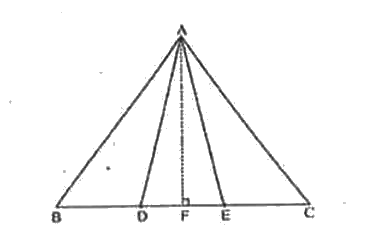
View SolutionIn the following Figure, D and E are two points on BC such that BD = DE = EC . Show that ar (ABD) = ar (ADE) = ar(AEC)
can you now answer the equation that you left in the "Introduction " of the capther, whether the filed of Budhia has been actually divided into three parts of equal area ?
View SolutionIn Fig.30D and E are to points on BC such that BD=DE=EC. Show that ar(ABD)=ar(ADE)=ar(AEC)
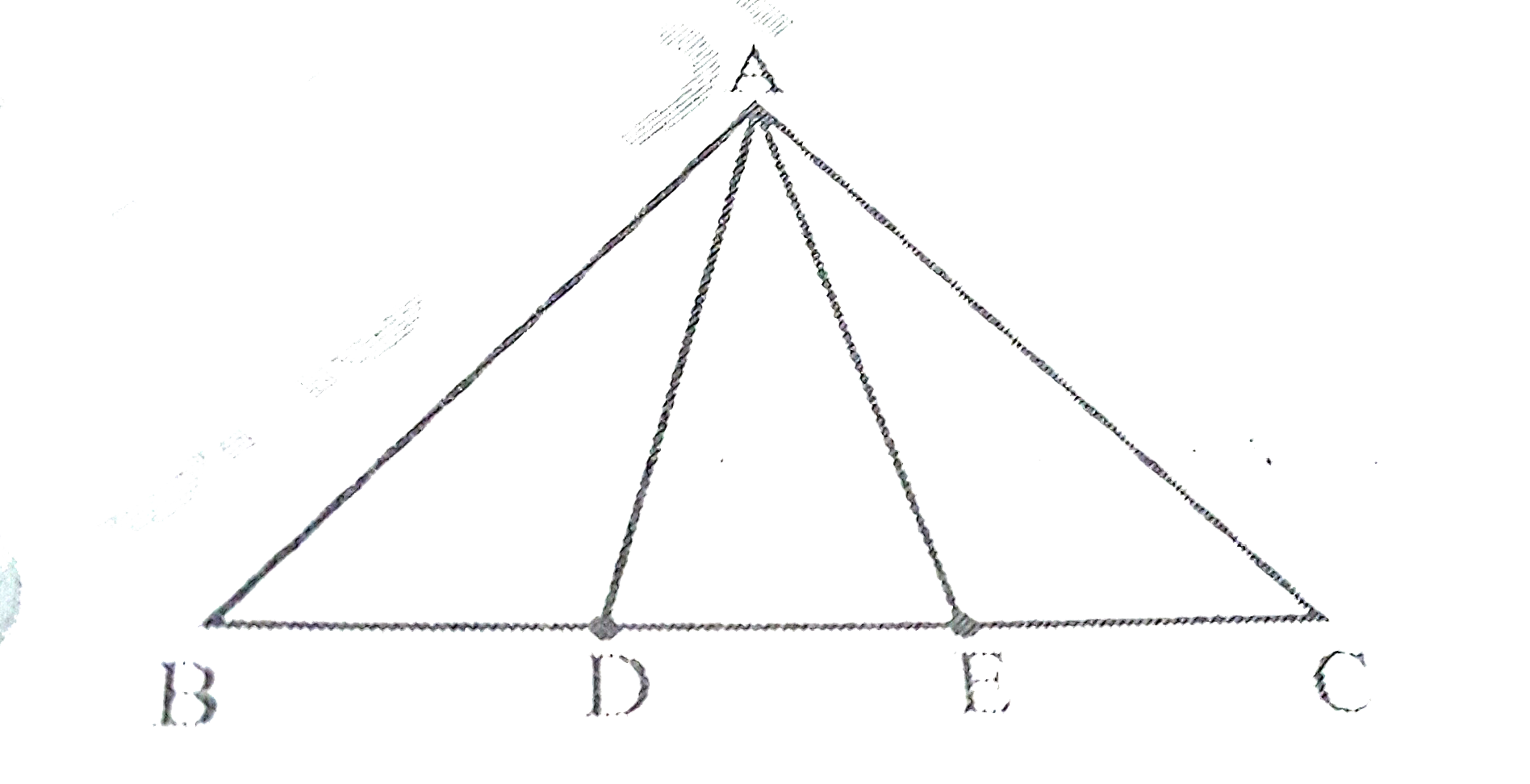
View Solutionदिए गए चित्र में भुजा BC पर दो बिंदु D और E इस प्रकार स्थित है की है| दर्शाइए की
है|
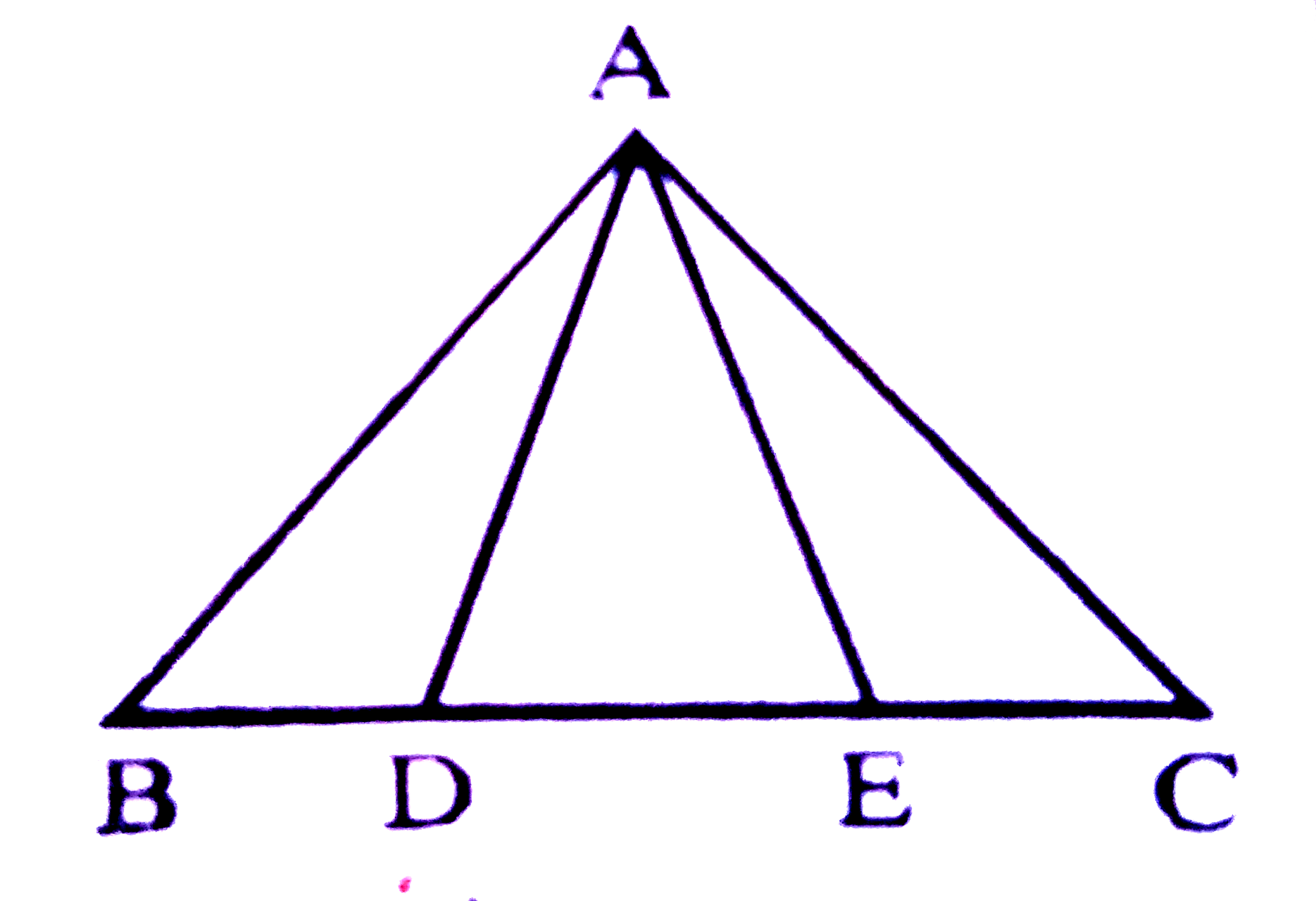
View Solutionआकृति में, भुजा BC पर दो बिन्दु D और E इस प्रकार स्थित है कि BD= DC= EC है। दर्शाइए कि ar (ABD) = ar (ADE) =ar (AEC) है।

View Solutionआकृति में, भुजा पर दो बिंदु और इस प्रकार स्थित है कि है। दर्शाइए कि है ।
क्या आप अब प्रश्न का उत्तर दे सकते है, जो आपने इस अध्याय की भूमिका में छोड़ दिया था कि क्या बुधिया का खेत वास्तव में बराबर क्षेत्रफलों वाले तीन भागो में विभाजित हो गया है?
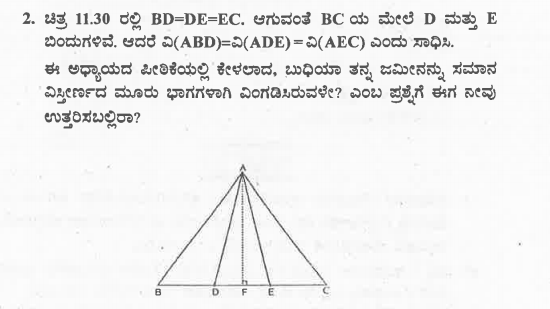
View Solutionಚಿತ್ರ ರಲ್ಲಿ BD = DE= EC, ಆಗುವಂತೆ BC ಯ ಮೇಲೆ D ಮತ್ತು E ಬಿಂದುಗಳಿವೆ. ಆದರೆ ವಿ(ABD)=ವಿ(ADE) =ವಿ(AEC) ಎಂದು ಸಾಧಿಸಿ. ಈ ಅಧ್ಯಾಯದ ಪೀಠಿಕೆಯಲ್ಲಿ ಕೇಳಲಾದ, ಬುಧಿಯಾ ತನ್ನ ಜಮೀನನ್ನು ಸಮಾನ ವಿಸ್ತೀರ್ಣದ ಮೂರು ಭಾಗಗಳಾಗಿ ವಿಂಗಡಿಸಿರುವಳೇ? ಎಂಬ ಪ್ರಶ್ನೆಗೆ ಈಗ ನೀವು ಉತ್ತರಿಸಬಲ್ಲಿರಾ?
View SolutionIn the given figure . If , , then find
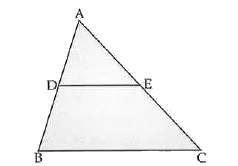
View SolutionIn the given figure, DE // BC.
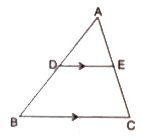
Given that , calculate DE, if BC = 45 cm.
Also , find
View SolutionIn Figure 1 DE|| BC ,AD = 1 cm and BD =2 cm . What is the ratio of the ar to the ?
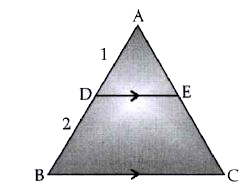
View SolutionIn DeltaABC , D and E are points on AB and AC respectively such that DE is parallel to BC. If AD= 2 cm, BD = 3 cm, then (ar(DeltaADE))/(ar(DeltaABC)) is
View SolutionABCD is a trapezium whose side AB is any point E. If AD || EC and DE || is BC, then ar( Delta DAE) : ar(DeltaBEC) Find out
View SolutionIn , D and E are points on AB and AC respectively such that DE||BC and DE divides the into two parts of equal areas. Then ratio of AD and BD is
View Solutionमें, बिंदु D तथा E, भुजा AB तथा AC पर इस प्रकार है की तथा DE, के क्षेत्रफल को दो बराबर भागो में बाटता है। AD तथा BD का अनुपात ज्ञात करे?
View SolutionIn the given figure, . If , find .
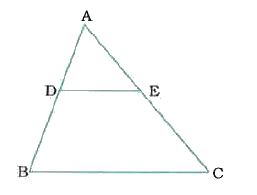
View SolutionIn the figure D, E are points on the sides AB and AC respectively of such that . Prove that DE || BC.
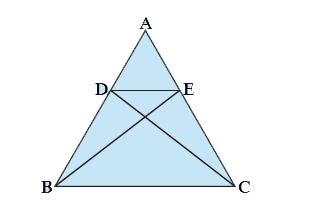
View SolutionIn the figure D, E are points on the sides AB and AC respectively of such that . Prove that DE || BC.
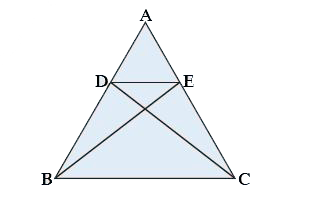
View SolutionIn the figure D, E are points on the sides AB and AC respectively of such that . Prove that DE || BC.
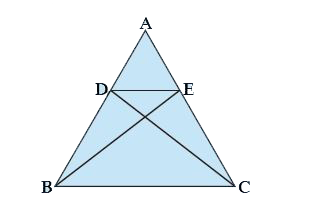
View SolutionDelta ABC A point D on BC is such that BD = ( 1)/( 3) DC Show that ar( Delta ABD ) = ( 1)/( 4) ar ( Delta ABC )
View SolutionD and E are points on sides AB and AC respectively of a such that ar . Show that .
View Solution