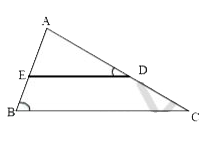
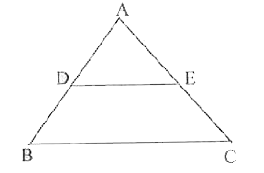
In the given figure if ∠ADE = ∠B show that ∆ADE ~ ∆ABC. If AD = 3.8cm AE = 3.6cm BE = 2.1cm and BC = 4.2cm find DE.
Given : ∠ABC and ∠A = ∠ALet DE be X cm Therefore by AA similarity theorem ∆ ADE - ∆ ABC
Related Solutions
In the given figure if /_ADE = /_B Then prove that DeltaADE - DeltaABC is. If AD = 3.8cm, AE = 3.6cm BE = 2.1 cm and BC = 4.2 cm, find the value of DE.
View SolutionIn the given figure, =
(i) Show that ABC ~ ADE
(ii) If AD = 3.8 cm, AE = 3.6cm, BE = 2.1 cm and BC = 4.2 cm, find DE.
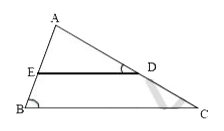
View SolutionIn the given figure, =
(i) Show that ABC ~ ADE
(ii) If AD = 3.8 cm, AE = 3.6cm, BE = 2.1 cm and BC = 4.2 cm, find DE.
View SolutionIn the given figure,
If AD = 3.8 cm, AE = 3.6cm,
BE = 2.1 cm and BC = 4.2 cm, Find DE.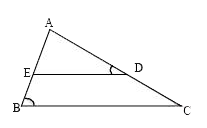
View SolutionIn , and . If AE = 2.1cm, then find AC.
View SolutionIn the given figure, , if and , then
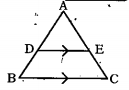
View SolutionIn the given figure, if , show that . If , find DE.
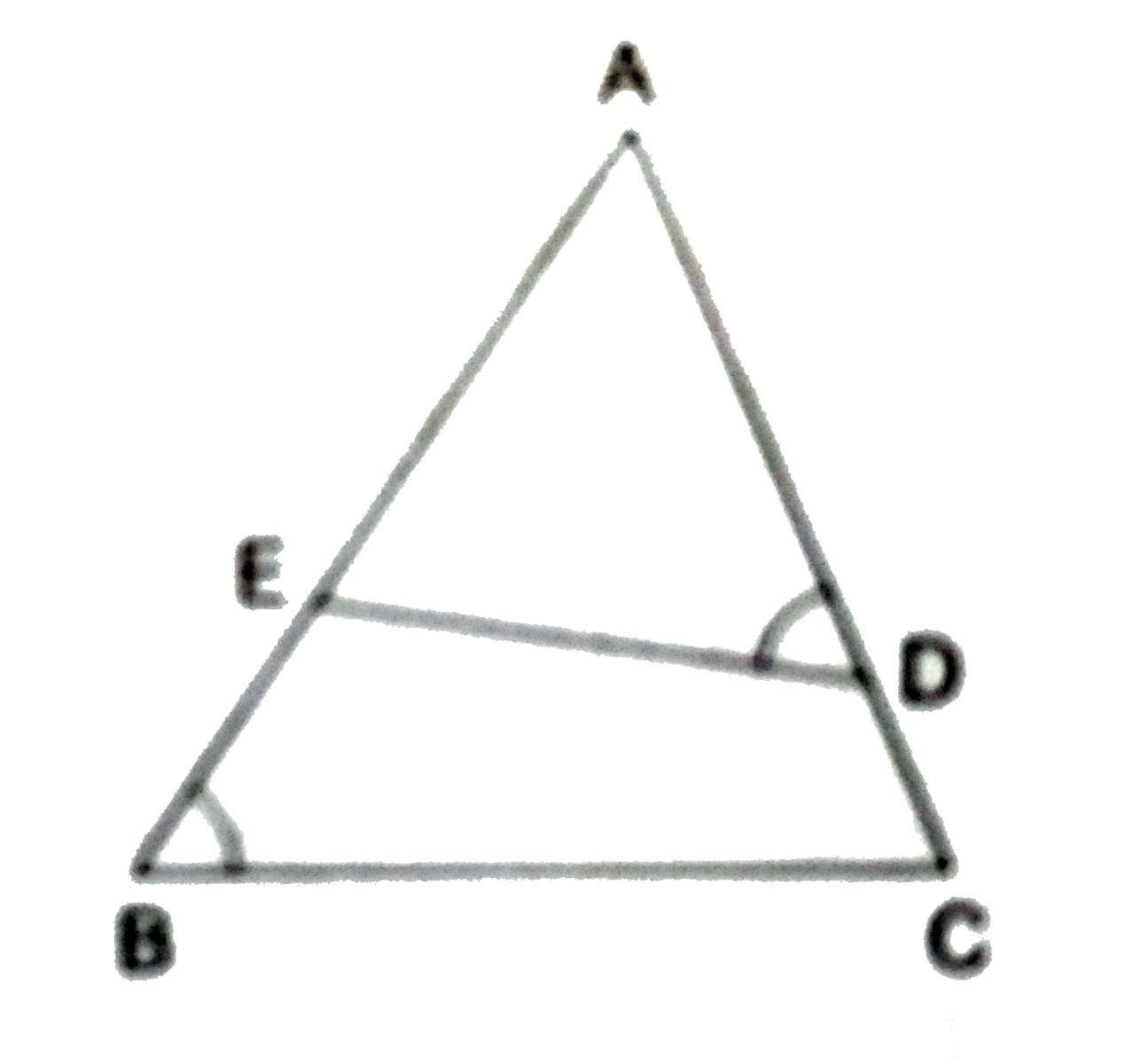
View SolutionIn ∆ABC, if ∠ADE = ∠B, then prove that ∆ADE ~ ∆ABC. Also, if AD = 7.6 cm, AE = 7.2 cm, BE = 4.2 cm and BC = 8.4 cm, then find DE.
View Solutionआक्रति में, AC -= AE, AB -= AD और -= है | दर्शाइए कि BC -= DE हिया |
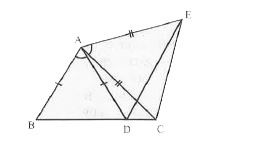
View SolutionIn the figure, AC = AE, AB = AD and BAD = EAC. Show that BC = DE

View SolutionIn the figure AC = AE, AB = AD and angleBAD = angleEAC . But show that BC = DE.
View SolutionIn the straight line parallel to intersects the other two sides at the points and respectively. If , and and , then
View SolutionIn the given figure, DE is parallel to the base BC of triangle ABC and AD: DB = 5: 3. Find the ratio :
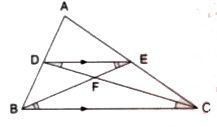
and then
View SolutionIn the given figure if then find length AD
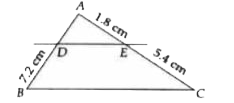
View SolutionIf then the length of AE=
View Solutionमें, तथा तब
View Solutionदी गयी आकृति में ABC एक त्रिभुज है यदि तो सिद्ध कीजिये
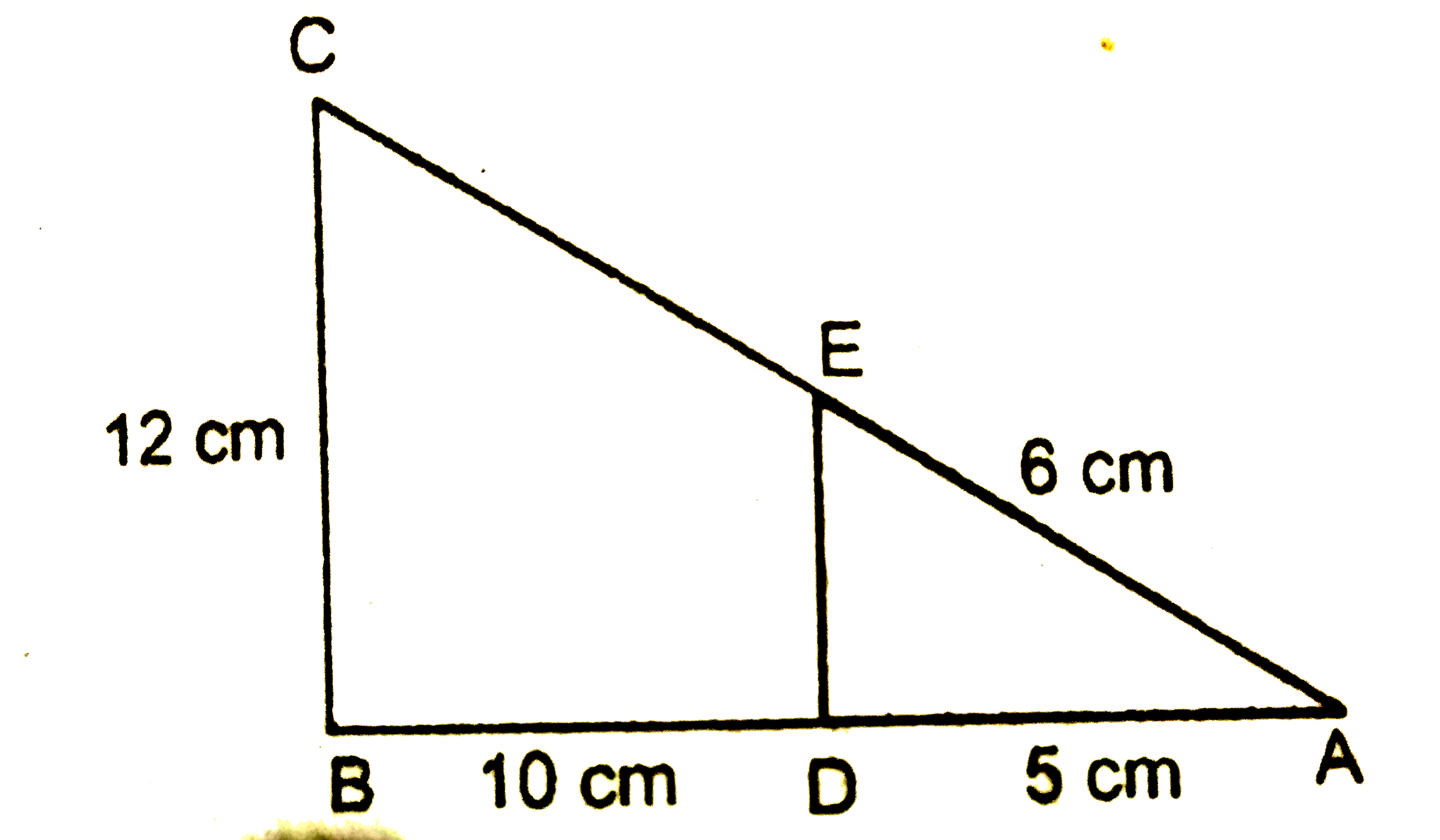
View Solutionदिए गए चित्र में तथा , तब EC और DE के मान ज्ञात करें ।
View SolutionABC is a triangle and DE is drawn parallel to BC cutting the other sides at D and E. If AB=3.6 cm, AC=2.4 cm and AD=2.1 cm, then AE is equal to :
View SolutionIn the given figure, DE // BC.

Prove that are similar
View Solution