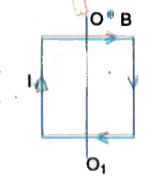
A square current carrying loop made of thin wire and having a mass 10g can rotate without friction with respect to the vertical axis OO1 passing through the centre of the loop at right angles to two opposite sides of the loop. The loop is pladed in a homogeneous magnetic field with an induction B = 10-1 T directed at the right angles to the plane of drawing . A current I = 2A is flowing in the loop. Find the period of oscillations that the loop performs about its position of stable equilibrium.
Consider a loop PQRS placed in uniform magnetic field B in such a way that the normal to coil subtends an angle θ to the direction of B when a current I flows through the loop clockwise. The sides PQ and RS are perpendicular to the field and equal and opposite forces of magnitude I and B act upwards and downwards respectively. Equal and opposite forces act on sides QR and PS towards right and left of coil. The resultant force is zero but resultant torque is not zero. The forces on sides PQ and RS produce a torque due to a single turn which is given by
Related Solutions
A square current carrying loop made of thin wire and having a mass m =10g can rotate without friction with respect to the vertical axis , passing through the centre of the loop at right angles to two opposite sides of the loop. The loop is placed in a homogeneous magnetic field with an induction directed at right angles to the plane of the drawing. A current I = 2A is flowing in the loop. Find the period of small oscillations that the loop performs about its position of stable equilibrium.
View SolutionA square current carrying loop made of thin wire and having a mass can rotate without friction with respect to the vertical axis passing throught the centre of the loop at right angles to two opposite sides of the loop. The loop is placed in a homogeneous magnetic field with and induction directed at right angles to the plane of the drawing current is flowing in the loop Find the period of small oscillations that the loop performs about its position of stable equilibrium
View SolutionA square current carrying loop made of thin wire and having a mass m=10g can rotate without friction with respect to the vertical axis OO_(1) passing throught the centre of the loop at right angles to two opposite sides of the loop. The loop is placed in a homogeneous magnetic field with and induction B =10^(-1)T directed at right angles to the plane of the drawing A current I=2A is flowing in the loop Find the period of small oscillations that the loop performs about its position of stable equilibrium
View SolutionA square loop of side a carris a current . The magnetic field at the centre of the loop is
View SolutionA square loop of side a carris a current I . The magnetic field at the centre of the loop is
View SolutionThe square loop ABCD , carrying a current i , is placed in uniform magnetic field B , as shown. The loop can rotate about the axis XX' . The plane of the loop makes and angle theta(theta lt 90^(@)) with the direction of B . Through what angle will the loop rotate by itself before the torque on it becomes zero
View SolutionThe square loop ABCD , carrying a current i is placed in a uniform magnetic field B, as shown. The loop can rotate about tha axis XX' . The plane of the loop makes an angle phi (phi lt 90^(@)) with the direction of B. Through what angle will the loop rotate by itself before the torque on it becomes zero ?
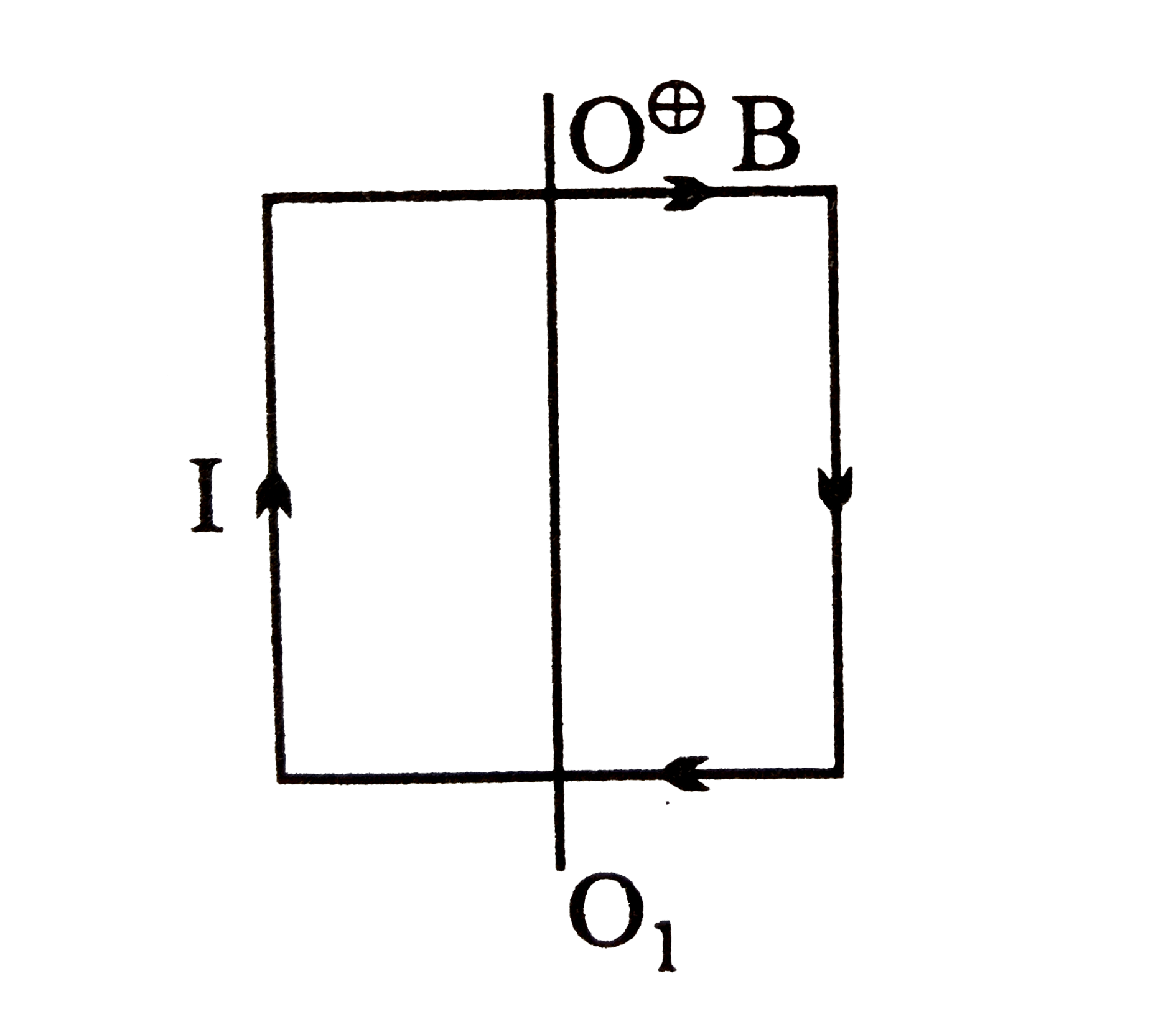
View SolutionA rectangular loop of wire shown below is coplanar with a long wire carrying current I.
 The loop is pulled to the right as indicated. What are the directions of the induced current in the loop and the magnetic forces on the left and the right sides of the loop
The loop is pulled to the right as indicated. What are the directions of the induced current in the loop and the magnetic forces on the left and the right sides of the loop
View SolutionEach side of a hexagonal loop of a metal wire is a. The loop carries a current I. Find the magnitude of the magnetic field at the centre of the loop
View SolutionA square loop of wire of side a carries a current i . Calculate the magnetic field at the centre of the loop
View SolutionA current carrying wire is in form of square loop of side length 10 cm. current in wire is 5A. Find out magnetic field at centre of loop.
View SolutionA square loop of edge 'a' carries a current l. The magnetic field at the centre of loop is
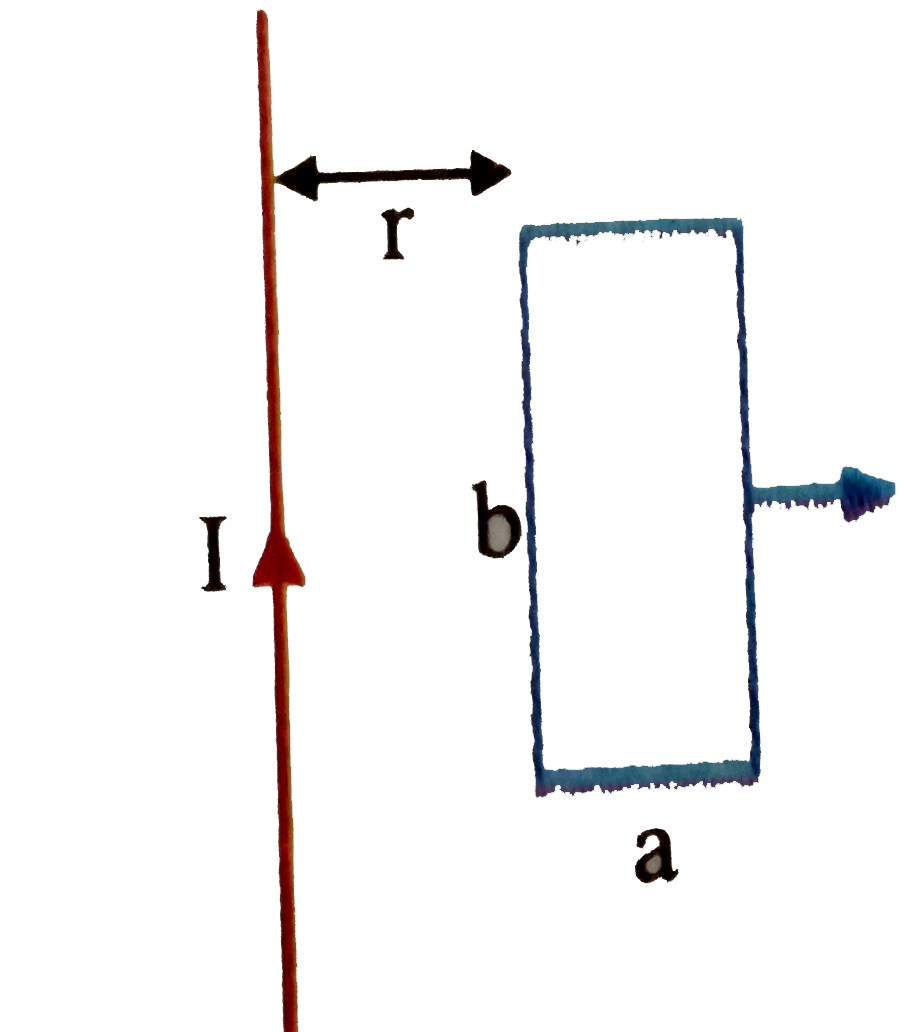
View SolutionA rectangular loop of wire with dimensions shown in figure is coplanar with a long wire carrying current . The distance between the wire and the left side of the loop is . The loop is pulled to the right as indicated. What are the directions of the induced current in the loop and the magnetic forces on the left and right sides of the loop when the loop is pulled ?
View SolutionA triangular loop of side 1 carries a current I. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
View SolutionA rectangular loop of wire with dimensions shown in figure is coplanar with a long wier carrying current 'I' . The distance between the wire and the left side of the loop is r . The loop is pulled to the right as indicated. What are the directions of the induced current in the loop and the magnetic forces on the left and right sides of the loop when the loop is pulled ?
View SolutionA square shape current loop of side length l and carrying current l lies in a uniform magnetic field B acting perpendicular to the plane of square loop and directed inward. The net magnetic force acting on current loop is
View SolutionA square loop of sides carries a current of .A uniform magnetic field of magnitude exists parallel to one of the side of the loop.(a)What is the force acting on the loop? (b)What is the torque acting on the loop?
View SolutionA square loop of sides 10 cm carries a current of 10 A .A uniform magnetic field of magnitude 0.20 T exists parallel to one of the side of the loop.(a)What is the force acting on the loop? (b)What is the torque acting on the loop?
View Solutionचित्र a में धारा लूप का चुंबकीय आघूर्ण ज्ञात कीजिये। लूप की प्रत्येक भुजा 10 सेमी तथा लूप में धारा 2.0 एम्पेयर हैं। तथा समकोण हैं।

View SolutionA wire loop is rotated in a uniform magnetic field about an axis perpendicular to the field. The direction of the current induced in the loop reverses in each
View Solution