A balloon starts rising from the surface of the Earth. The ascension rate is constant and equal to vo. Due to the wind the balloon gathers the horizontal velocity component vx = ay where a is a constant and y is the height of ascent. Find how the following quantities depend on the height of ascent: a the horizontal drift of the balloon x y; b the total tangential and normal accelerations of the balloon.
According to the problemHence
Related Solutions
A balloon starts rising from the earth's surface. The ascension rate is constant and equal to v_(0) . Due to the wind. The balloon gathers the horizontal velocity component v_(x)=ky , where k is a constnat and y is the height of ascent. Find how the following quantities depednd on the height of ascent. (a) the horizontal drift of the balloon x (y) (b) the total tangential and normal accelrations of the balloon.
View SolutionA balloon starts rising from the earth's surface. The ascension rate is constant and equal to v_(0) . Due to the wind. The balloon gathers the horizontal velocity component v_(x)=ky , where k is a constnat and y is the height of ascent. Find how the following quantities depednd on the height of ascent. (a) the horizontal drift of the balloon x (y) (b) the total tangential and normal accelrations of the balloon.
View SolutionA balloon starts rising from the surface of the earth with vertical component of velocity v_(0) . The balloon gathers a horizontal velocity v_(x) = ay , where a is a constant and y is the height from the surface of the earth, due to a horizontal wind. Determine (a) the equation of trajectory of the balloon. (b) the tangential, normal and total acceleration of the balloon as function of y.
View SolutionA balloon starts rising from the surface of the Earth. The ascertion rate is constant and equal to . Due to the wind the balloon
View SolutionA balloon starts rising from the surface of the earth with a verticle component of velocity v_(0) . The baloon gathes a horizontal velocity v_(x)=lambda_(y) , where lambda is a constant and y is the height from the surface of earth, due to a horizontaln wind. determine (a) the equation of trajectory and (b) the tangential, normal and total acceleration of the balloon as a function of y .
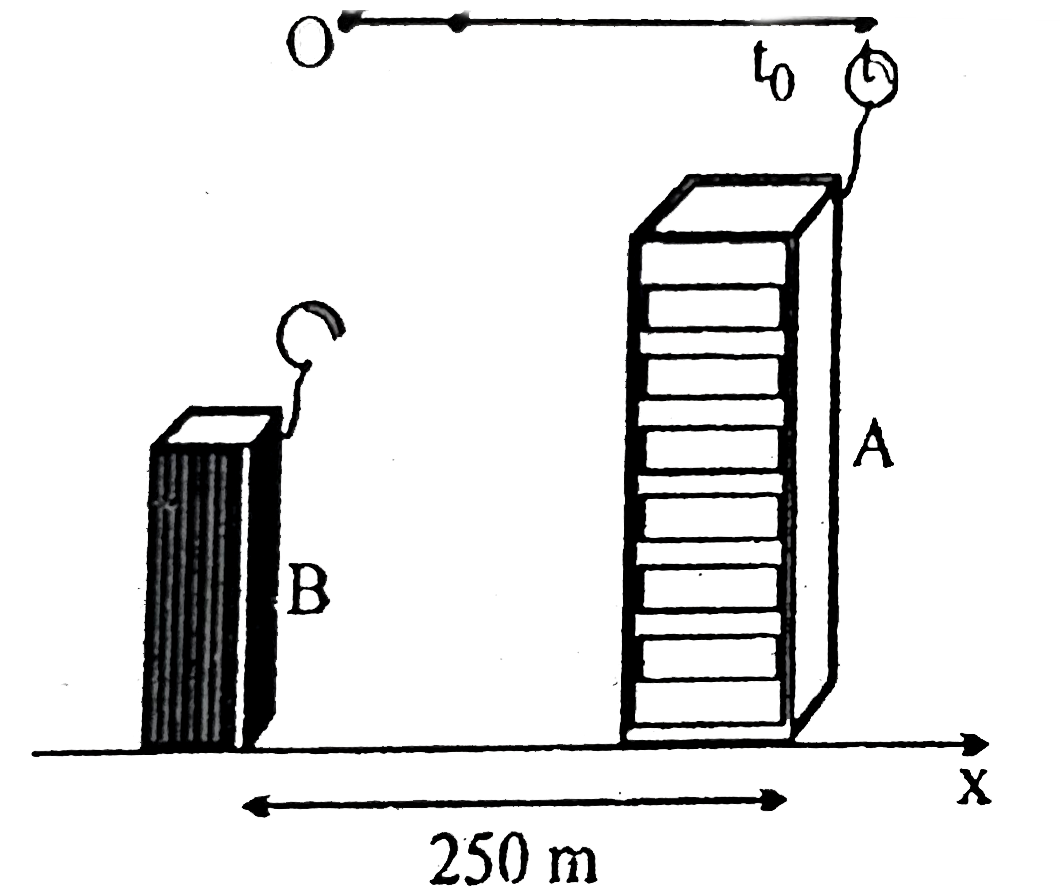
View SolutionTwo ballons are simultaneously released from two buildings A and B. Balloon from A rises with constant velocity While the other one rises with constant velocity of Due to wind the balloons gather horizontal velocity y, where 'y' is the height from the point of release. The buildings are at a distance of m & after some time 't' the balloons collide.
View SolutionA body, thrown from the balloon reached the ground in 30 seconds. If the balloon is moving upwards with constant velocity of , then find the height of the balloon at that time.
View Solutionएक गुब्बारा 215 मीटर लम्बे तार से बंधा है तथा क्षैतिज से का कोण बनाता है|गुब्बारे की जमीन से ऊंचाई ज्ञात कीजिए|
View SolutionAn observer spots a balloon moving with the wind in a horizontal line at a height of 105 m from the ground. The angle of elevation of the balloon after sometime reduces from 60% to 30%. Find the distance travelled by the balloon during the interval.
View SolutionOn the surface of the earth at 1 atm pressure, a balloon filled with gas occupies 500mL. This volume is of its maximum capacity. The balloon is left in air. It starts rising. The height above which the balloon will burst if temperature of the atmospere remains constant and the pressure decreases 1 mm for every 100cm rise of height is:
View SolutionA particle is released from a certain height H = 400m . Due to the wind, the particle gathers the horizontal velocity component v_x = ay "where a "= (sqrt5)s^(-1) and y is the vertical displacement of the particle from the point of release, then find (a) the horizontal drift of the particle when it strikes the ground , (b) the speed with which particle strikes the ground.
View SolutionA particle is released from a certain height H = 400m . Due to the wind, the particle gathers the horizontal velocity component v_x = ay "where a "= (sqrt5)s^(-1) and y is the vertical displacement of the particle from the point of release, then find (a) the horizontal drift of the particle when it strikes the ground , (b) the speed with which particle strikes the ground.
View SolutionA balloon rises from rest on the ground with constant acceleration g / 8. A stone is dropped from the balloon when the balloon has risen to a height of (H). Find the time taken by the stone to reach the ground.
View Solutionfrom a balloon (3)/(2)g rising up with a constant velocity k, a stone is dropped which reaches the earth, (25)/(2)g gets the velocity. The height of the balloon while releasing the stone was:
View SolutionAn inflated balloon rises to a definite height once its starts going up .This balloon cannot rise any further because at that height :
View Solutionएक गुब्बारा, जिसकी डोर 20 मी लम्बी है आकाश में उड़ रहा है यदि डोर क्षैतिज से का कोण बनाती हो, तो गुब्बारे की ऊँचाई होगी
View Solutionएक गुब्बारा, जिसकी डोर 20 मी लम्बी है आकाश में उड़ रहा है यदि डोर क्षैतिज से का कोण बनाती हो, तो गुब्बारे की ऊँचाई होगी
View SolutionA balloon whose string is 20 m long is flying in the sky. If the door is horizontal 45^(@) then the height of the balloon will be
View SolutionThe rope of a balloon flying in the air is 60 m long. rope horizontally 30^(@) makes an angle. What will be the height of the balloon?
View SolutionAssertion : A balloon stops rising after attaining a certain maxium height .
Reason : Upthrust due to air decreases with height till it just balances the weight of the balloon.
View Solution