Determine if 25110 is divisible by 45.[Hint: 5 and 9 are co-prime numbers. Test the divisibility of the number by 5 and 9.]
The prime factorization of 45 = 5 x 925110 is divisible by 5 as ‘0’ is at its unit place.25110 is divisible by 9 as sum of digits is divisible by 9.Therefore the number must be divisible by 5 x 9 = 45
Related Solutions
Determine if 25110 is divisible by 45.[Hint:5 and 9 are co-oprime numbers.Test the divisibility of the numbers by 5 and 9.].
View SolutionDetermine if 25110 is divisible by 45.
View SolutionDetermine if 25110 is divisible by 45.
View SolutionA number is divisible by both 5 and 12.By which other number will that number be always divisible?
View SolutionUsing divisibility tests, determine which of the following numbers are divisible by 5 :179015
View SolutionWithout dividing, find whether the number 25110 is divisible by 45.
View Solutionबिना भाग किए ज्ञात कीजिए की क्या 25110 संख्या 45 से विभाज्य है!
View SolutionCheck whether 25110 is divisible by 45.
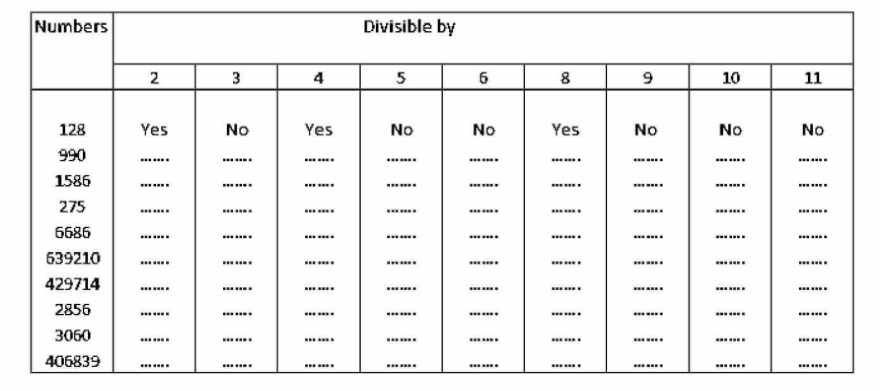
View SolutionUsing divisibility tests, determine which of the following numbers are divisible by 2;by 3; by 4; by 5; by 6; by 8; by 9; by 10 ; by 11 (say, yes or no):
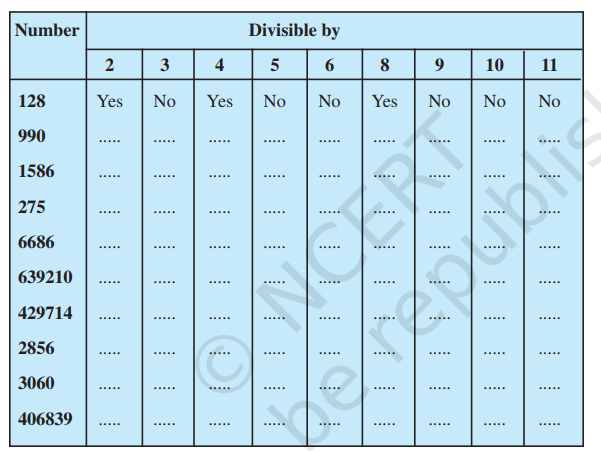
View SolutionUsing divisibility tests, determine which of the following numbers are divisible by 2;by 3; by 4; by 5; by 6; by 8; by 9; by 10 ; by 11 (say, yes or no):
View Solution100 और 200 के बीच के उन पूर्णांकों का योग ज्ञात कीजिए, जो
(i) 9 से विभाज्य हैं।
(ii) 9 से विभाज्य नहीं है।
[संकेत (ii) : ये संख्याएँ होंगी : कुल संख्याएँ -9 से विभाज्य संख्याएँ ]
View SolutionCheck the divisibility of the given numbers, as indicated. Using tests for divisibility.
459827 by 9
View SolutionUsing the tests of divisibility, find which of the following numbers are,
divisible by 9
View SolutionWhich of the following statements are true? If a number is divisible by 3, it must be divisible by 9. If a number is divisible by 9, it must be divisible by 3. If a number is divisible by 4, it must be divisible by 8. If a number is divisible by 8, it must be divisible by 4. If a number is divisible by 18, if it is divisible by both 3 and 6. If a number is divisible by both 9 and 10, it must be divisible by 90. If a number exactly divides the sum of two numbers, it must exactly divide the numbers separately. If a number divides three numbers exactly, it must divide their sum exactly. If two numbers are co-prime, at least one of them must be a prime number. The sum of two consecutive odd numbers is always divisible by 4.
View SolutionWhich of the following statements are true? If a number is divisible by 3, it must be divisible by 9. If a number is divisible by 9, it must be divisible by 3. If a number is divisible by 4, it must be divisible by 8. If a number is divisible by 8, it must be divisible by 4. If a number is divisible by 18, if it is divisible by both 3 and 6. If a number is divisible by both 9 and 10, it must be divisible by 90. If a number exactly divides the sum of two numbers, it must exactly divide the numbers separately. If a number divides three numbers exactly, it must divide their sum exactly. If two numbers are co-prime, at least one of them must be a prime number. The sum of two consecutive odd numbers is always divisible by 4.
View SolutionTotal number of 9-digit numbers that are divisible by 5 is equal to
View Solutionयदि एक संख्या 9 से विभाज्य है, तो वह 3 से भी विभाज्य होगी का प्रतिधनात्मक कथन है -
View SolutionA number divisible by 9 is also divisible by:
View Solutionএকটি সবচেয়ে ছোট সংখ্যা বার করো যা 8 ও 9 দ্বারা বিভাজ্য। 8 ও 9 এর ল.সা.গু নির্ণয় করো।
View SolutionUsing divisibility tests, determine which of the following numbers are divisible by 2, by 3, by 4, by 5, by 6, by 8, by 9, by 10, by 11 (say, yes or no).
Number = 128,990,1586,275,6686,639210,429714,2856,3060,406839
View Solution