Two fixed identical conducting plates α &β each of surface area S are charged to –Q and q respectively where Q > q > 0. A third identical plate γ free to move is located on the other side of the plate with charge q at a distance d Fig 1.13. The third plate is released and collides with the plate β . Assume the collision is elastic and the time of collision is sufficient to redistribute charge amongst β &γ . a Find the electric field acting on the plate γ before collision. b Find the charges on β and γ after the collision. c Find the velocity of the plate γ after the collision and at a distance d from the plate β.
b During the collision plates α & β are together and hence must be at one potential. Suppose the charge on β is q1 and on γ is q2. Consider a point O. The electric field here must be zero.Thus the charge on β and γ are Q + q/2 and q/2 respectively.c Let the velocity be v at the distance d after the collision. If m is the mass of the plate γ then the gain in K.E. over the round trip must be equal to the work done by the electric field. After the collision the electric field at γ isThe work done when the plate γ is released until the collision is F1d where F1 is the force on plate γ.The work done after the collision till it reaches d is F2d where F2 is the force on plate γ.
Related Solutions
Two fixed identical conducting plates (alpha and beta) , each of surface areas S are charged to -Q and q, respectively, where Q>q>0. A third identical plate (y), free to move is located on the other side of the plate which charge q at a distance d. The third platea in released and colides with the plate beta . Assume the collision is elastic and the time of collision is sufficient to redistribute charge amongest beta and gamma . Find the electric field acting on the plate gamma before collision.
View SolutionTwo fixed identical conducting plates (alpha and beta) , each of surface areas S are charged to -Q and q, respectively, where Q>q>0. A third identical plate (y), free to move is located on the other side of the plate which charge q at a distance d. The third platea in released and colides with the plate beta . Assume the collision is elastic and the time of collision is sufficient to redistribute charge amongest beta and gamma . Find the charges on beta and gamma after the collision.
View SolutionTwo fixed, identical conducting plates , each of surface area S are charged to -Q and q, respectively, where Q q 0. A third identical plate , free to move is located on the other side of the plate with charge Q at a distance d (figure). The third plate is released and collides with the plate . Assume the collision is elastic and the time of collision is sufficient to redistribute charge amongst .
(a) Find the electric field acting on the plate before collision.
(b) Find the charges on after the collision.
(c) Find the velocity of the plate after the collision and at a distance d from the plate
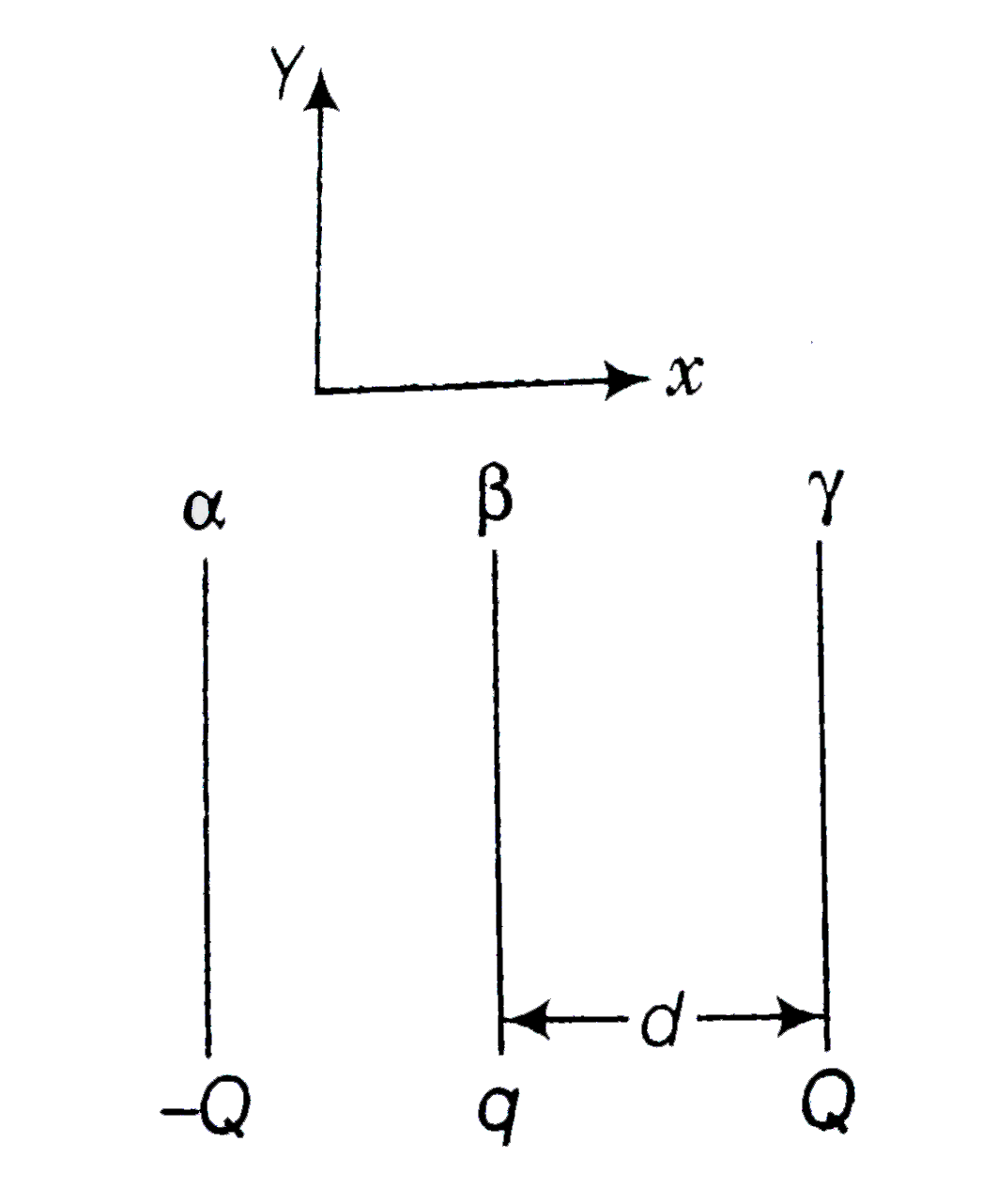
View SolutionTwo fixed, identical conducting plates (a and (3), each of surface area S are charged to - Q and q, respectively, where Q > q > 0. A third identical plate ( lambda ), free to move Is located on the other side of the plate with charge q at a distance d as per figure. The third plate is released and collides with the plate f_3 . Assume the collision is elastic and the time of collision is sufficient to redistribute charge amongst beta and gamma . (a) Find the electric field acting on the plate gamma before collision. (b) Find the charges on beta and gamma after the collision. (c) Find the velocity of the plate gamma after the collision and at a distance d from the plate beta
View SolutionTwo fixed, identical conducting plates (alpha and beta) , each of surface area S are charged to -Q and q , respectively, where Q gt q gt 0 . A third indentical plate (gamma) , free to move is located on the other side of the plate with charge q at a distance d, fig. The third plate is released and collidies with the plate beta . Assume the collsion is electric and the time of collision is sufficient to redistribute charge amongst beta and gamma . (a) Find the electric field acting on the plate gamma before collision. (b) Find the charge on beta and gamma after the collision. (c) Find the velocity of the plate gamma after the collision and at a distance d from the plate beta .
View Solutionएक समानान्तर प्लेट संधारित्र को बैटरी से जोड़ा गया है। इसके धनात्मक प्लेट A एवं ऋणात्मक प्लेट B पर आवेश क्रमशः एवं है। एक तीसरी प्लेट, C, A एवं B के समरूप जिस पर आवेश है, को दोनों प्लेट के बीच में उसके समानान्तर रखा गया है?
View SolutionTwo metal plates X and Y of the area A are separated by a distance .d. The plates are charged +Q and -Q respectively. This arrangement is called…………………………..
View SolutionWhat is the force of attraction between the two plates of a parallel plate capacitor? Assume that, area of each plate of the capacitor is A and one plate is charged with +Q and the other with -Q.
View SolutionForce between two conducting large plates , with charges Q and Q/2 as shown in the figure, is (Area of each face of plate =A)
View SolutionForce between two conducting large plates , with charges Q and as shown in the figure, is (Area of each face of plate =A)
_PHY_E01_022_Q01.png)
View SolutionThree identical metal square plates of surface area A of each side is arranged as shown in the figure.Plates 1 2 and 3 are given charges +20, -Q and -Q respectively. Find out the correct options A) Charge on the two faces of the middle plate are -2Q and Q B) Charge on the two faces of the middle plate are -Q and 0 C) Charge on the two faces of the left most plate are zero and 2Q D) Charge on the two faces of the right most plate are -Q and zero
View SolutionThe plates of a charged parallel plate capacitor attract each other by a force F= ____________, where q = charge on each plate and A = area of each plates.
View Solutionकिसी समांतर पट्टिका सधारित्र के लिए, प्लेटो का क्षेत्रफल =A प्लेटो के बीच दुरी =d प्लेटो पर आवेश +Q तथा -Q है। यदि प्लेटो के बीच आकर्षण-बल F हो, तब
View Solutionएक समांतर प्लेट संधारित्र में, प्लेट का क्षेत्रफल A तथा आवेश Q है। अन्य प्लेट पर आवेश के कारण एक प्लेट पर लगने वाला बल बराबर होगा :
View Solutionएक समांतर प्लेट वायु संधारित्र, जिसका प्लेट क्षेत्रफल A और प्लेट पृथक्करण d है, के प्रत्येक प्लेट को एक धनात्मक आवेश q दिया जाता है, तो:
View SolutionA positive charge q is given to each plate of a parallel plate air capacitor having plate area A and plate separation d, then
View Solution
Two large parallel conducting plates of net charge and are placed in a uniform external electric field prependicular to plates as shown. The surface area of each plates is A. The charge on the left surface of the left plate and right surface of the right plate are respectively.
View SolutionTwo large parallel conducting plates of net charge 2Q and -Q are placed in a uniform external electric field (Q)/(2Aepsilon_(0)) prependicular to plates as shown. The surface area of each plates is A. The charge on the left surface of the left plate and right surface of the right plate are respectively.
View SolutionA parallel-plate capacitor is connected to a cell. Its positive plate and its negative plate have charges and respectively. A third plate , identical to and , with charge , is now introduced midway between and , parallel to them. Which of the following are correct?
View SolutionA parallel-plate capacitor is connected to a cell. Its positive plate A and its negative plate B have charges +Q and -Q respectively. A third plate C , identical to A and B , with charge +Q , is now introduced midway between A and B , parallel to them. Which of the following are correct?
View Solution