Let P1x = x2 + a1x + b1 and P2x = x2 + a2x + b2 be two quadratic polynomials with integer coeffcients. Suppose a1 ≠ a2 and there exist integers m ≠ n such that P1m = P2n P2m = P1n. Prove that a1 - a2 is even.
We have m2 + a1m + b1 = n2 + a2n + b2 n2 + a1n + b1 = m2 + a2m + b2. Hence a1 - a2m + n = 2b2 - b1; a1 + a2m - n = 2n2 - m2.This shows that a1 + a2 = -2n + m. Hence 4b2 - b1 = a22 - a21. Since a1 + a2 and a1 - a2 have same parity it follows that a1 - a2 is even.
Related Solutions
If (1+x-3x^(2))^(2145)=a0+a1x+a2x^(2)+... then a0-a1+a2-a3+...... ends with
View SolutionIf the equation of the locus of a point equidistant from the points (a_1, b_1) and (a_2, b_2) is (a_1-a_2)x+(b_1-b_2)y+c=0 , then the value of c is a a2-a2 2+b1 2-b2 2 sqrt(a1 2+b1 2-a2 2-b2 2) 1/2(a1 2+a2 2+b1 2+b2 2) 1/2(a2 2+b2 2-a1 2-b1 2)
View SolutionIf the equation of the locus of a point equidistant from the points and is , then the value of is
View SolutionA(a1, b1) மற்றும் B(a2, b2) ஆகிய புள்ளிகளை இணைக்கும் கோட்டுத் துண்டை X-அச்சு எந்த விகிதத்தில் பிரிக்கும்?
View Solutionসংখ্যারেখা তৈরি করে নীচের সংখ্যাগুলিকে সংখ্যারেখায় দেখাও ও নাম দাও। +5, -2, +3, -6, +2, -5, -এ যথাক্রমে A,B,C,D,E ও F নাম দাও। B থেকে E-এর দূরত্ব কত ঘর মেপে দেখো।
View SolutionSuppose A1,A2,…..A30 are thirty sets each having 5 elements and B1,B2,…….Bn are n sets each having 3 elements.Let each elements of S belongs to exactly 10 of A1,'s and exactly 9 of B1's.Then find the value of n.
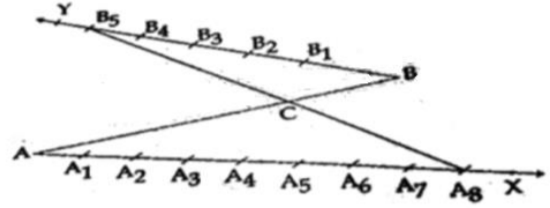
View SolutionIn the figure, if B1, B2, B3,…... and A1,A2, A3,….. have been marked at equal distances. In what ratio C divides AB?
View SolutionIf x,y,z are in A.P.and A1 is the arithmetic mean of x,y and A2 is the arithmetic mean of y,z then prove that the arithmetic mean of A1 and A2 isy
View SolutionIf and be the first, second and third ionization constant of and . Then which is/are correct ?
View SolutionThe activation energies of two raction are and with . If the temperature of the reacting systems is increased from to predict which of the following alternatives is correct
View SolutionThe activation energies of two reactions are and with . If the temperature of the reacting systems is increased from to , which of the following is correct?
View SolutionThe activation energies of two reactions are E_(a1) and E_(a2) with E_(a1) gt E_(a2) . If the temperature of the reacting systems is increased from T_(1) to T_(2) predict which of the following alternatives is correct
View SolutionThe activation energies of two reactions are E_(a1) and E_(a2) with E_(a1) gt E_(a2) . If the temperature of the reacting systems is increased from T to T' , which of the following is correct?
View SolutionA reactant (A) forms two products : A overset (k_1) rarr B , Activation energy, E_(a1) Aoverset (k_2) rarr C , Activation energy, E_(a2) If E_(a2) = 2E_(a1) , then k_1 and k_2 are related as
View SolutionThe activation energies of two reactions are E_(a1) and E_(a2) with E_(a1) gt E_(a2) . If the temperature of the reacting systems is increased from T to T' , which of the following is correct?
View SolutionIf are arithmetic means inserted between the numbers a and b, then find the value of
View Solutionजल में के लिए क्यों है?
View SolutionThe ratios a1/a2 , b1/b2 , c1/c2 Find out whether the given linear equations are pairwise compatible or incompatible: 2x - 3y = 8 and 4x - 6y = 9.
View SolutionEvaluate:
View SolutionLet , then a1, a2, a3 is in
View Solution