In the adjoining figure AP and BP are angle bisector of ∠A and ∠B which meet at a point P of the parallelogram ABCD. Then 2∠APB = A ∠A + ∠B B ∠A + ∠C C ∠B + ∠D D ∠C + ∠D
The correct option is D.
Related Solutions
In Figure, is a parallelogram in which . If the bisectors of and meet at prove that and Figure
View SolutionIn Figure, is a parallelogram in which . If the bisectors of and meet at prove that and Figure
View SolutionIn a quadrilateral . The bisectors of meet at the point P. The measure of is
View SolutionIn a quadrilateral ABCD, . The bisectors of meet at the point P. The measure of is
View SolutionIn a quadrilateral ABCD angle D = 60^(@) And angle C = 100^(@) Is. angle A And angle B The bisectors of s meet at point P. angle APB is the measure of
View Solutionis a parallelogram and If the bisectors and of angles and respectively, meet at on prove that is the mid-point of
View SolutionIn Figure, is a parallelogram and If the bisectors and of angles and respectively, meet at on prove that is the mid-point of
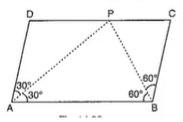
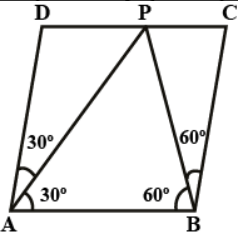
View SolutionIf AP and BP are the bisectors of the angle A and angle B of a parallelogram ABCD, then value of the angle APB is
View SolutionIn Figure, is a parallelogram and . If the bisectors of angles respectively, meet at on prove that is the mid-point of .
View SolutionIn Figure, is a parallelogram and If the bisectors of angles respectively, meet at on prove that is the mid-point of
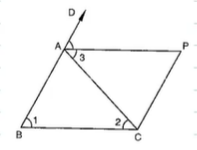
View SolutionIn figure and is the bisector of exterior of . Prove that (ii) is a parallelogram
View SolutionIn figure and is the bisector of exterior of . Prove that
(i)
(ii) is a parallelogram
View SolutionIn parallelogram ABCD angle bisector of C and D meet each other at angle
View SolutionIn parallelogram ABCD, the bisector of angle A meets DC at P and AB = 2AD.
Prove that :
(i) BP bisects angle B.
(ii) Angle APB =
View SolutionThe bisector of interior of meets in and the bisector of exterior meets produced in Prove that
View SolutionIn Figure, is an isosceles triangle in which and is the bisector of exterior of . Prove that and (ii) is a parallelogram.
View SolutionIn Figure, is an isosceles triangle in which and is the bisector of exterior of . Prove that and (ii) is a parallelogram.
View SolutionThe bisector of of an isosceles triangle with meets the circumcircle of at as shown in Figure. If produced meet at prove that .
View SolutionIn Figure, is a parallelogram in which is the mid-point of is a point on such that . If produced meets prove that is a mid-point of .
View SolutionIn figure D is a point on side BC of a such that . Prove that AD is the bisector of .

View Solution