In the adjoining figure AP and BP are angle bisectors of ∠A and ∠B which meets at P on the parallelogram ABCD. Then 2∠APB = A ∠C + ∠D B ∠A + ∠C C ∠B + ∠D D 2∠C
The correct option is A.
Related Solutions
In Figure, is a parallelogram in which . If the bisectors of and meet at prove that and Figure
View SolutionIn Figure, is a parallelogram in which . If the bisectors of and meet at prove that and Figure
View SolutionIn a quadrilateral . The bisectors of meet at the point P. The measure of is
View SolutionIn a quadrilateral ABCD, . The bisectors of meet at the point P. The measure of is
View SolutionIn a quadrilateral ABCD angle D = 60^(@) And angle C = 100^(@) Is. angle A And angle B The bisectors of s meet at point P. angle APB is the measure of
View SolutionIn parallelogram ABCD angle bisector of C and D meet each other at angle
View Solutionis a parallelogram and If the bisectors and of angles and respectively, meet at on prove that is the mid-point of
View SolutionIn figure and is the bisector of exterior of . Prove that (ii) is a parallelogram
View SolutionIn figure and is the bisector of exterior of . Prove that
(i)
(ii) is a parallelogram
View SolutionIn Figure, is a parallelogram and . If the bisectors of angles respectively, meet at on prove that is the mid-point of .
View SolutionIn Figure, is a parallelogram and If the bisectors of angles respectively, meet at on prove that is the mid-point of
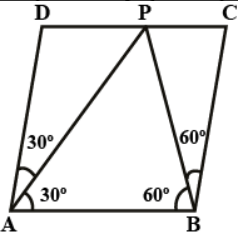
View SolutionIf AP and BP are the bisectors of the angle A and angle B of a parallelogram ABCD, then value of the angle APB is
View SolutionIn Figure, is an isosceles triangle in which and is the bisector of exterior of . Prove that and (ii) is a parallelogram.
View SolutionThe bisector of interior of meets in and the bisector of exterior meets produced in Prove that
View SolutionIf a,b,c ,d are distinct integer in AP such that , then a+b+c+d is
View SolutionIn Figure, is an isosceles triangle in which and is the bisector of exterior of . Prove that and (ii) is a parallelogram.
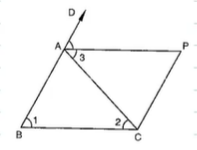
View SolutionIn Figure, is a parallelogram and If the bisectors and of angles and respectively, meet at on prove that is the mid-point of
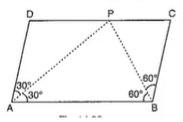
View SolutionThe bisector of of an isosceles triangle with meets the circumcircle of at as shown in Figure. If produced meet at prove that .
View SolutionIn Figure, find the four angles in the parallelogram
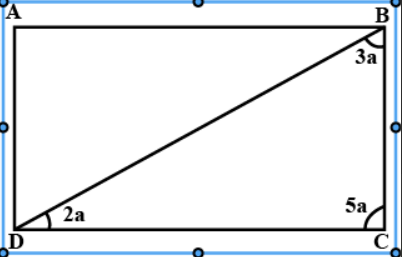
View SolutionIn Figure, find the four angles in the parallelogram
View Solution