If there are three or more parallel lines and the intercepts made by them on a transversal are equal then the corresponding intercepts on any other transversal are also equal. Prove that.
Three parallel lines I m and n i.e. I ║ m ║ n. A transversal p meets these parallel lines are points A B and C respectively such that AB = BC. Another transversal q also meets parallel lines I m and n at points D E and F respectively. To Prove: DE = EF Construction: Through point A draw a line parallel to DEF; which meets BE at point P and CF and point Q. Proof: In ∆ACQ B is mid-point of AC and BP is parallel to CQ and we know that the line through the midpoint of one side of the triangle and parallel to another side bisects the third side. ∴ AP = PQ ...i When the opposite sides of a quadrilateral are parallel it is a parallelogram and so its opposite sides are equal. ∴ AP ║ DE and AD ║ PE ⇒ APED is a parallelogram. ⇒ AP = DE ....ii And PQ ║ EF and PE ║ QF ⇒ PQFE is a parallelogram ⇒ PQ = EF ....iii From above equations we get DE = EF
Related Solutions
If there are three parallel lines, and the intercepts made by them on one transversal are equal, then the intercepts on any other transversal are also equal.
View SolutionIf there are three parallel lines, and the intercepts made by them on one transversal are equal, then the intercepts on any other transversal are also equal.
View SolutionIf three or more parallel lines are intersected by two transversal; Prove that the intercepts made by them on tranversal are propotional.
View Solutionl, m and n are three parallel lines intersected by the transversals p and q at A, B, C and D,E, F such that they make equal intercepts AB and BC on the transversal p. Show that the intercepts DE and EF on q are also equal.
View Solutionl, m and n are three parallel lines intersected by the transversals p and q at A, B, C and D,E, F such that they make equal intercepts AB and BC on the transversal p. Show that the intercepts DE and EF on q are also equal.
View Solutionl, m and n are three parallel lines intersected by the transversals p and q at A, B, C and D,E, F such that they make equal intercepts AB and BC on the transversal p. Show that the intercepts DE and EF on q are also equal.
View Solutionl, m and n are three parallel lines intersected by the transversals p and q at A, B, C and D,E, F such that they make equal intercepts AB and BC on the transversal p. Show that the intercepts DE and EF on q are also equal.
View Solutionl, m and n are three parallel lines intersected by the transversals p and q at A, B, C and D,E, F such that they make equal intercepts AB and BC on the transversal p. Show that the intercepts DE and EF on q are also equal.
View Solutionएक तिर्यक रेखा दो समांतर रेखाओं को प्रतिच्छेद करती है। सिद्ध कीजिए कि इस प्रकार बने संगत कोणों के युग्म के समद्विभाजिक समान्तर होते है।
View SolutionIf two parallel lines are cut by a transversal then corresponding angles are equal.
View SolutionIf a transversal intersects two parallel line then corresponding angles are an necessarily equal.
View Solutionयदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार प्रतिच्छेद करें कि संगत कोणों के एक युग्म के समद्विभाजक परस्पर समान्तर हो, तो सिद्ध कीजिए कि दोनों रेखायें भी परस्पर समान्तर होती हैं |
View Solutionयदि तीन या अधिक समान्तर रेखाओ को दो तिर्यक-चेदि रेखाएँ प्रतिच्छेद करती है तो सिद्ध कीजिए कि इनके द्वारा तिर्यक-छेदीरेखाओ पर बनाए गए अंत:खंड अनुपातिक होते है ।
View SolutionIf two parallel lines are cut by a transversal then corresponding angles are equal.
View SolutionAngles made by the transversal#!# Transversal of Parallel Lines
View Solutionl, m and n are three parallel lines intersected by transversals p and q such that l, m and n cut off equal intercepts AB and BC on p (see Fig. 8.28). Show that l, m and n cut off equal intercepts DE and EF on q also.
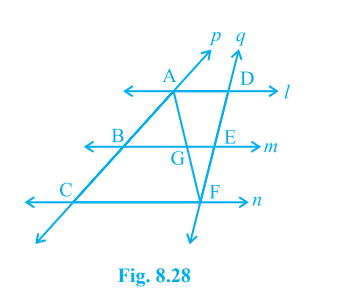
View Solutionl, m and n are three parallel lines intersected by transversals p and q such that l, mand n cut off equal intercepts AB and BC on p (see Fig. 8.28). Show that l, m and n cut off equal intercepts DE and EF on q also
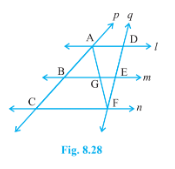
View Solutionl, m and n are three parallel lines intersected by transversals р and q such that l , m and n cut off equal intercepts AB and BC on p (see the given figure). Show that l, m and n cut off equal intercepts DE and EF on q also.
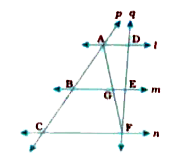
View Solutionl, m and n are three parallel lines intersected by transversals p and q such that l, m and n cut off equal intercepts AB and BC on p (see Fig.). Show that l, m and n cut off equal intercepts DE and EF on q also
View Solutionl, m and n are three parallel lines intersected by transversals p and q such that l, m and n cut off equal intercepts AB and BC on p (see Figure). Show that l, m and n cut off equal intercepts DE and EF on q also.
View Solution