ABCD is a rhombus and P Q R and S are the mid-points of the sides AB BC CD and DA respectively. Prove that the quadrilateral PQRS is a rectangle.
According to the given statement the figure will be a shown alongside; using mid-point theorem:- In ∆ABC PQ ║ AC and PQ = 1/2 AC ....i In ∆ADC SR ║ AC and SR = 1/2 AC ....ii ∴ P = SR and PQ ║ SR [From i and ii] ⇒ PQRS is a parallelogram. Now PQRS will be a rectangle if any angle of the parallelogram PWRS is 900 PQ ║ AC [By mid-point theorem] QR = BD [By mid-point theorem] But AC ⊥ BD [Diagonals of a rhombus are perpendicular to each other] ∴ PQ ⊥ QR [Angle between two lines = angles between their parallels] ⇒ PQRS is a rectangle
Related Solutions
ABCD एक समचतुर्भुज है। AB,BC,CD,DA के मध्य-बिंदु क्रमशः P,Q,R,S हैं। सिद्ध कीजिए कि PQRS एक आयत है।
View SolutionABCD is a rectangle and P,R and S are the mid - points of the AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionABCD is a rhombus and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
View SolutionABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
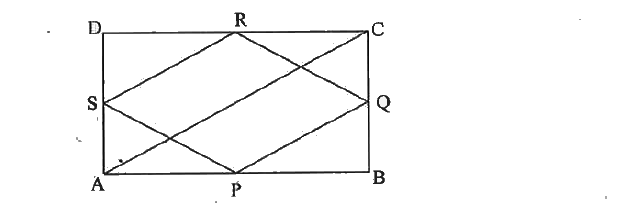
View SolutionABCD is a rectangle and P,Q,R and S are the mid points of the sides AB,BC,CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionABCD is a rhombus and P, Q, R and S are wthe mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
View SolutionABCD is a rectangle and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionABCD is a rhombus and P, Q, R, S are the mid-points of AB, BC, CD and DA respectively. Prove that quadrilateral PQRS is a rectangle.
View SolutionABCD is a rectangle and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionABCD is a rectangle and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionABCD is a rhombus and P, Q, R, S are the mid-points of AB, BC, CD and DA respectively. Prove that quadrilateral PQRS is a rectangle.
View SolutionP, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View SolutionP, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View SolutionP,Q,R and S are respectively the mid points of the sides AB,BC,CD and DA of a quadrilateral ABCD such that ACbotBD . Prove that PQRs is a rectangle.
View SolutionABCD is a rhombus and P,Q,R and S are the mid points of the sides AB,BC,CD and DA. Show that the quadrilateral PQRS is a rectangle.
View SolutionABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionABCD is a rhombus and are the mid-points of respectively. Prove that is a rectangle.
View SolutionLet ABCD be a rectangle. If the mid-points of the sides AB, BC, CD, DA are respectively P, Q, R, S, then what is the quadrilateral PQRS?
View SolutionLet ABCD be a rectangle. Let P, Q, R, S be the mid-points of sides AB, BC, CD, DA respectively. Then the quadrilateral PQRS is a
View Solution