In the given figure ΔABC is isosceles with AB = AC. D E and F are respectively the mid-points of ides BC CA and AB. Show that the line segment AD is perpendicular to the line segment EF and is bisected by it.
Given : ΔABC is isosceles with AB = AC E and F are the mid-point of BC CA and AB.To prove : AD⟂ EF and is bisected by itConstruction : Join D E and FProof: DE||AC and DE =1/2 ABand DF||AE and DF =1/2 AC[Line segment joining mid-points of two sides of a triangle is parallel to the third side and is half of it.]
Related Solutions
In given Fig.
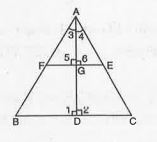 , is isosceles with AB = AC. D, E, F are the mid-points of sides BC, AC and AB respectively. Show that the line segment AD is perpendicular to the line segment EF and is bisected by it.
, is isosceles with AB = AC. D, E, F are the mid-points of sides BC, AC and AB respectively. Show that the line segment AD is perpendicular to the line segment EF and is bisected by it.
View SolutionIn given Fig.
 ,
,
is isosceles with AB = AC. D, E, F are the mid-points of sides BC, AC and AB respectively. Show that the line segment AD is perpendicular to the line segment EF and is bisected by it.
View SolutionThe sides AB and AC are equal of an isosceles triangle ABC. D E and F are the mid-points of sides BC, CA and AB respectively. Prove that:
(i) Line segment AD is perpedicular to line segment EF.
(ii) Line segment AD bisects the line segment EF.
View SolutionThe sides AB and AC are equal of an isosceles triangle ABC. D E and F are the mid-points of sides BC, CA and AB respectively. Prove that:
(i) Line segment AD is perpedicular to line segment EF.
(ii) Line segment AD bisects the line segment EF.
View Solutionयदि की भुजाओं BC,CA और AB के मध्यबिंदु क्रमशः D,E और F हों तो सिद्ध कीजिए कि AD रेखाखंड EF को समद्विभाजित करती है।
View Solutionएक समद्विबाहु त्रिभुज है जिसमें और F क्रमश: BC,CA और AB के मध्य बिंदु हैं । सिद्ध करें कि रेखाखण्ड AD रेखाखण्ड FE पर लम्ब होगा और उससे समद्विभाजित होगा।
View Solutionएक रेखाखंड AB पर AD और BC दो बराबर लंब रेखाखंड है। दर्शाइए कि CD , रेखाखंड AB को समद्विभाजित करता है।

View SolutionIn F are mid-points of the sides BC, CA and AB respectively . Show that :
AD is perpendicular to EF.
View Solutionमाना कि ABC एक समद्विबाहु त्रिभुज हैं, जहाँ AB=AC तथा D,E तथा F क्रमशः BC,CA तथा AB के मध्य-बिंदु हैं, तो सिद्ध करें कि AD EF तथा EF ,AD को समद्विभाजित करती है।
View Solutionएक रेखाखण्ड AB पर AD और BC दो बराबर लम्ब रेखाखण्ड है | ( देखीए आकृति ) | दर्शाइए कि CD, रेखाखण्ड AB को समद्धिभाजीत करता है |
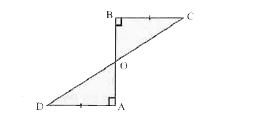
View Solutionएक रेखाखंड AB पर AD और BC दो बराबर लंब रेखाखंड हैं (देखिए आकृति)। दर्शाइए कि CD, रेखाखंड AB को समद्विभाजित करता है।
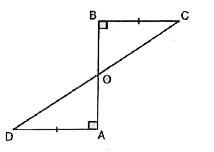
View Solutionमान लीजिए एक समबाहु त्रिभुज है जिसमे यदि भुजाओं तथा के मध्य-बिन्दुओं क्रमशः हो, तो सिद्ध कीजिए की रेखाखण्ड तथा परस्पर समकोण पर प्रतिच्छेद करते है।
View Solutionਰੇਖਾਖੰਡ AB 'ਤੇ AD ਅਤੇ BC ਲੰਬ ਹਨ(ਵੇਖੋ ਚਿੱਤਰ 7.18)। ਸਿੱਧ ਕਰੋ ਕਿ CD ਰੇਖਾ ਖੰਡ AB ਨੂੰ ਸਮਦੁਭਾਜਿਤ ਕਰਦੀ ਹੈ।
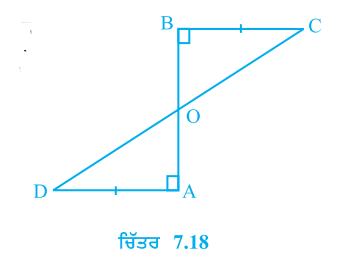
View SolutionAD and BC are equal perpendiculars to a line segment AB (see the given figure) Show that CD bisects AB.
View SolutionIn F are mid-points of the sides BC, CA and AB respectively . Show that :
AD and FE bisect each other.
View SolutionAD एक समद्धिबाहू त्रिहुज ABC का एक शीर्षलम्ब है, जिसमे AB -= AC है | दर्शाइए कि
(i) AD रेखाखण्ड BC को समद्धिभाजित करता है |
(ii) AD कोण A को समद्धिभाजित करता है |
View SolutionAD एक समद्विबाहु त्रिभुज ABC का एक शीर्षलम्ब है, जिसमें AB = AC है। दर्शाइए कि
(i) AD रेखाखंड BC को समद्विभाजित करता है। (ii ) AD कोण A को समद्विभाजित करता है।
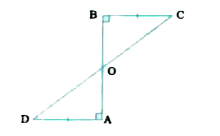
View SolutionIn the given figure, AD and BC are equal perpendicualrs to a line segment AB.
Show that CD bisects AB.
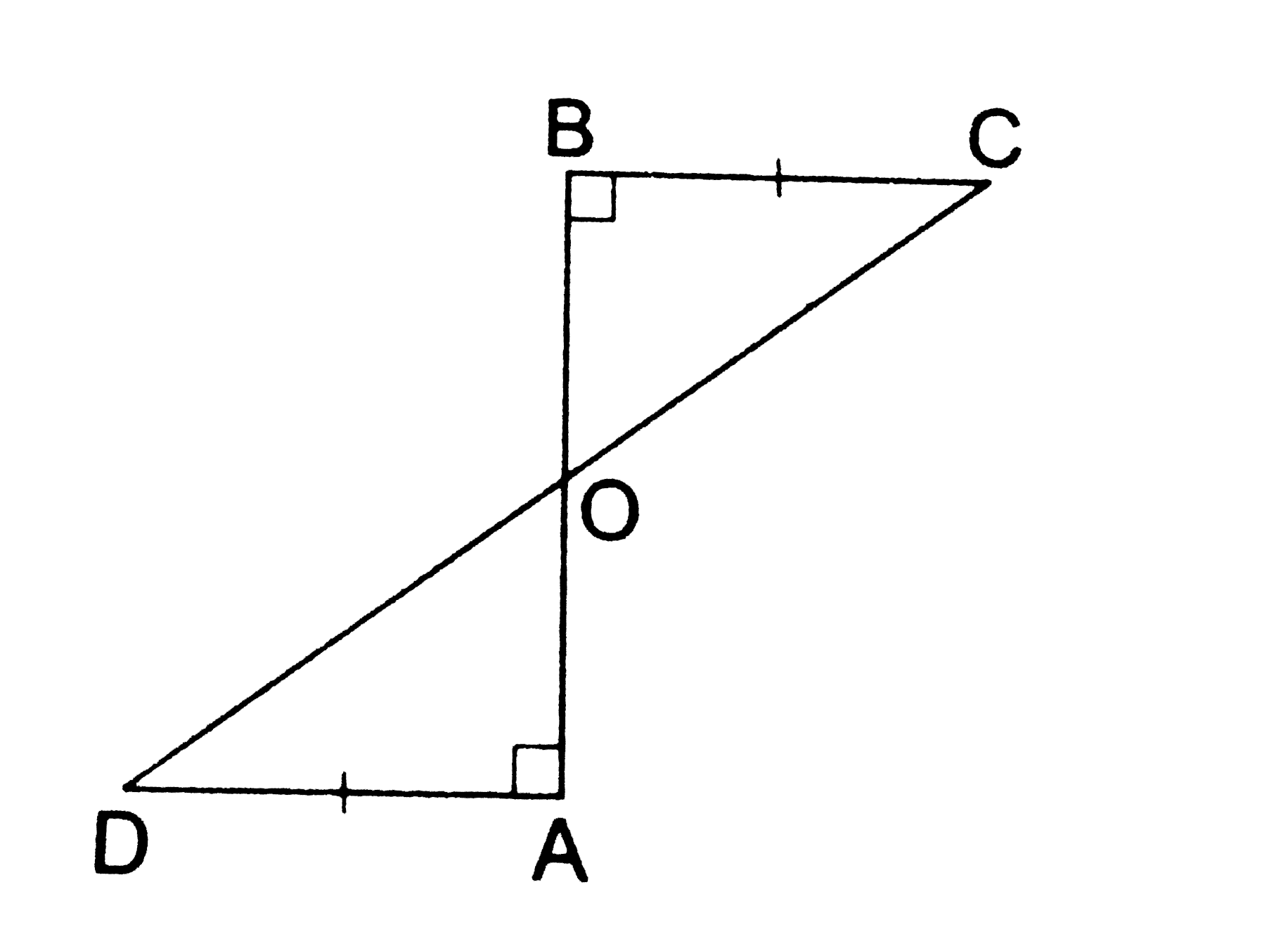
View SolutionAD and BC are equal perpendiculars to a line segment AB. If AD and BC are on different sides of AB prove that CD bisects AB.
View Solutionबिन्दु D, E, F क्रमशः त्रिभुज की भुजाओ BC, CA और AB के मध्य-बिन्दु है। सिद्ध करे कि AD, EF को समद्विभाजित करता है।
View Solution