Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
Given : A rhombus ABCD whose diagonals intersect each other at O. To prove : A circle with AB as diameter passes through O. Proof : ∠AOB = 90° [Diagonals of a rhombus bisect each other at 90°] ⇒ ∆AOB is a right triangle right angled at O. ⇒ AB is the hypotenuse of A B right ∆AOB. ⇒ If we draw a circle with AB as diameter then it will pass through O. because angle is a semicircle is 90° and ∠AOB = 90° Proved.
Related Solutions
Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
View SolutionProve that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
View SolutionProve that the circle drawn with any side of a rhombus as diameter, passes through the point of intersection of its diagonals.
View SolutionProve that the circle drawn with any side of a rhombus as diameter, passes through the point of intersection of its diagonals.
View Solutionसिद्ध कीजिए कि किसी समचतुर्भुज की किसी भुजा को व्यास मानकर खींचा गया वृत्त उसके विकर्णों के प्रतिच्छेद बिंदु से होकर जाता है ।
View SolutionProve that the circle drawn with any side of a rhombus as a diameter, posses through the point of intersection of its diagonals.
View Solutionसिद्ध कीजिए कि किसी समचतुर्भुज कि किसी भुजा को व्यास मानकर खिंचा गया वृत्त उसके विकर्णों के प्रतिच्छेद बिन्दु से होकर जाता है |
View Solutionसिध्द कीजिए की किसी चतुर्भज की किसी भुजा को व्यास मानकर खींचा गया वृत्त उसके विकर्णों के प्रतिच्छेद बिंदु से होकर जाता है।
View Solutionವಜ್ರಾಕೃತಿಯ ಒಂದು ಬಾಹುವನ್ನು ವ್ಯಾಸವಾಗಿರುವಂತೆ ಒಂದು ವೃತ್ತವನ್ನು ರಚಿಸಿದರೆ, ಅದು ಕರ್ಣಗಳು ಛೇದಿಸುವ ಬಿಂದುವಿನ ಮೂಲಕ ಹಾದುಹೋಗುತ್ತದೆ ಎಂದು ಸಾಧಿಸಿ.
View SolutionProve that the two circles drawn on the two equal sides of an isosceles triangle as diameters pass through the mid point of the third side.
View SolutionA circle is passing through three vertices of a rhombus of side 8 cm and its centre is the fourth gest diagonal of the rhombus ( in cm).
View SolutionIf two circles are drawn taking any two sides to the triangle as diameter then prove that point of intersection of two circles lies on the third side.
View SolutionIf circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
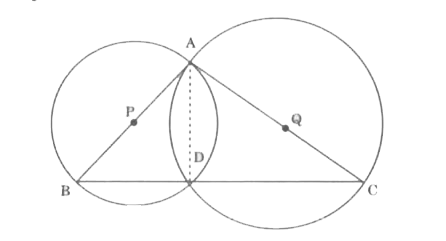
View SolutionIf circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
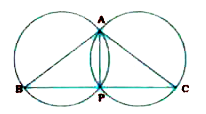
View SolutionIf circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
View SolutionIf circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.

View SolutionIf circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side
View SolutionProve that all the circles drawn in diameter on all four sides of an equilateral parallelogram pass through a common point.
View SolutionProve that the circles drawn by the equilateral sides of an isosceles triangle as diameters pass through the midpoint of the third side.
View SolutionIf two intersecting chords of a circle make equal angles with the diameterpassing through their point of intersection, prove that the chords are equal
View Solution