Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Given : Two equal chords AD and CE of a circle with centre O. When meet at B when produced. To Prove : ∠ABC = 1/ 2 ∠AOC – ∠DOE Proof : Let ∠AOC = x ∠DOE = y ∠AOD = z ∠EOC = z [Equal chords subtends equal angles at the centre] ∴ x + y + 2z = 36° [Angle at a point] .. i OA = OD ⇒ ∠OAD = ∠ODA ∴ In DOAD we have ∠OAD + ∠ODA + z = 180° ⇒ 2∠OAD = 180° – z [ ∠OAD = ∠OBA] ⇒ ∠OAD = 90° – z/ 2 ... ii Similarly ∠OCE = 90° – z/ 2 ... iii ⇒ ∠ODB = ∠OAD + ∠ODA [Exterior angle property] ⇒ ∠OEB = 90° – z/ 2 + z [From ii] ⇒ ∠ODB = 90° + z/ 2 ... iv Also ∠OEB = ∠OCE + ∠COE [Exterior angle property] ⇒ ∠OEB = 90° – z/ 2 + z [From iii] ⇒ ∠OEB = 90° + z/ 2 ... vAlso ∠OED = ∠ODE = 90° – y/ 2 ... vi O from iv v and vi we have ∠BDE = ∠BED = 90° + z/ 2 – 90° − y/ 2⇒ ∠BDE = ∠BED = y/ z + 2 ⇒ ∠BDE = ∠BED = y + z ... vii ∴ ∠BDE = 180° – y + z ⇒ ∠ABC = 180° – y + z ... viii Now y − z/2 = 360o - y -2z - y / 2= 180° – y + z ... ix From viii and ix we have ∠ABC = x- y / 2 Proved
Related Solutions
Let vertex of an angle ABC be located outside a circle and let the sides of the angle intersect chords AD and CE with the circle. Prove that is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
View SolutionLet the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that is equal to half the difference of the angles subtended by the chords AC and DE at the centre
View SolutionLet the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle.Prove that /_ABC is equal to half of the difference of the angles subtended by the chords AC and DE at the center.
View Solutionमान लीजिए कि कोण ABC का शीर्ष एक वृत्त के बाहर स्थित है और कोण कि भुजाएँ वृत्त से बराबर जीवाएँ AD और CE कटती हैं | सिद्ध कीजिए कि जीवाओं AC तथा DE द्वारा केन्द्र पर अंतरित कोणों के अंतर का आधा है |
View SolutionLet the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
View SolutionLet the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
View Solutionमान लीजिए कि कोण ABC का शीर्ष एक वृत्त के बाहर स्थित है और कोण की भुजाएँ वृत्त से बराबर जीवाऍ AD और CE काटती है। सिद्ध कीजिए कि जिवाओ AC तथा DE द्वारा केंद्र पर अंतरित कोणों के अंतर का आधा है ।
View Solutionमान लीजिए की कोण ABC का शीर्ष वृत्त के बहार स्थित है और कोण की भुजाएँ वृत्त से बराबर जीवाएं AD और CE कटती है। सिध्द कीजिए की जीवाओं AC और DE द्वारा केंद्र पर अंतरित कोनो के अंतर का आधा है।
View SolutionProve that if chords of congruent circles subtend equal angles at their centres then chords are equal.
View SolutionIf the angles subtended by two chords of a circle at the centre are equal, then Prove chords are equal.
View SolutionProve that, "If chords of congruent circles subtend equal angles at their centre, then the chords are equal."
View SolutionProve that if chords of congruent circles subtend equal angles at their centre then the chords are equal.
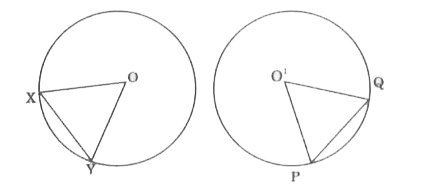
View SolutionProve that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
View SolutionIf the angles subtended by the chords of a circle at the centre of the circle are equal, then the chords are equal.
View SolutionEqual chords of a circle subtend equal angles at the centre.
View SolutionEqual chords of a circle subtend equal angles at the centre.
View SolutionEqual chord of circle subtends equal angle on centre.
View SolutionProve that equal chords of congruent circles subtend equal angles at their centre.
View SolutionProve that equal chords of a circle subtend equal angles at the centre.
View SolutionProve that equal chords of congruent circles subtend equal angles at their centre.
View Solution