Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection
Given : Two intersecting circles in which OO′ is the line of centres and A and B are two points of intersection. To prove : ∠OAO′ = ∠OBO′ Construction : Join AO BO AO′ and BO′. Proof : In ∆AOO′ and ∆BOO′ we have AO = BO [Radii of the same circle] AO′ = BO′ [Radii of the same circle] OO′ = OO′ [Common] ∴ ∆AOO′ ≅ ∆BOO′ [SSS axiom] ⇒ ∠OAO′ = ∠OBO′ [CPCT] Hence the line of centres of two intersecting circles subtends equal angles at the two points of intersection. Proved.
Related Solutions
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection
View SolutionProve that the line of centres of two intersecting circles subtends equal angles at the two points of intersection
View SolutionProve that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
View SolutionProve that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
View SolutionProve that the line of centres of two intersecting circles subtends equal angles at the two point of intersection.
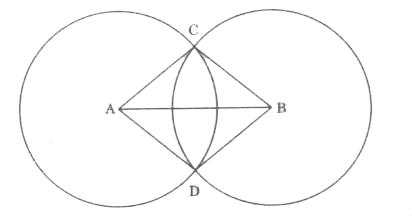
View SolutionProve that the line segment joining the centres of two intersecting circles subtends equal angles at the two points of intersection.
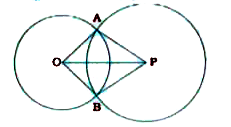
View SolutionProve that the line joining centres of two interesting circles subtends equal angles at the two points of intersection.
View SolutionProve that the line of centres of two interesting circles subtends equal angles at the two points of intersection.
View SolutionThe line of centres of two intersecting circles subtends equal angles at the two points of intersection.
View SolutionA circle (with centre at O) is touching two intersecting lines AX and BY. The two points of contact A and B subtend an angle of at any point C on the circumference of the circle. If P is the point of intersection for the two lines, then the measure of is :
View SolutionIf two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
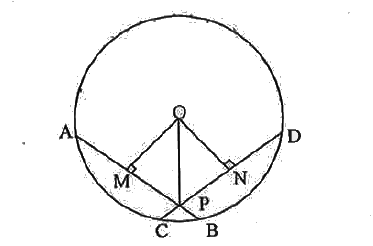
View SolutionIf two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the center makes equal angles with the chords.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
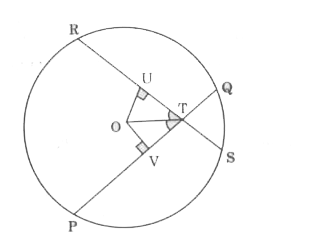
View SolutionIf two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chord.
View SolutionA circle (with centre at O) is touching two intersecting lines AX and BY. The two points of contact A and B subtend an angle of at any point C on the circumference of the circle. If P is the point of intersection for the two lines, then the measure of is :
View SolutionA circle (with centre at O) is touching two intersecting lines AX and BY. The two points of contact A and B subtend an angle of at any point C on the circumference of the circle. If P is the point of intersection for the two lines, then the measure of is :
View SolutionProve that the line between the centers of two intersecting circles produces equal angles at the point at which they intersect.
View Solutionसिद्ध कीजिए किसी वृत्त की दो बराबर जीवाओं के प्रतिच्छेदन बिन्दु को केन्द्र से मिलाने वाला रेखाखण्ड, जीवाओं से अन्तरित कोण को अर्द्धित करता है।
View Solution