A particle of mass m and charge q is projected into a region having a perpendicular magnetic field B. Find the angle of deviation figure 34-E14 of the particle as it comes out of the magnetic field if the width d of the region is very slightly smaller thana mv/qB b mv/2qB c 2mv/qB.
Mass of the particle = m Charge = q Width = da If d = mV/qBThe d is equal to radius. θ is the angle between theradius and tangent which is equal to π/2 As shown in the figureb If ≈ mV/2qB distance travelled = 1/2 of radiusAlong x-directions d = VXt [Since acceleration in this direction is 0. Force acts along j directions]Looking into the figure the angle between the initial direction and final direction of velocity is π.
Related Solutions
A particle of mass m and charge q is projected into a region having a perpendicular magnetic field B. Find the angle of deviation of the particle as it comes out of the magnetic field if the width d of the region is slightly less than.
(

View SolutionA particle of mass m and charge q is projected into a region having a perpendicular magnetic field B. Find the angle of deviation of the particle as it comes out of the magnetic field if ihe width d of the region is

View SolutionA particle of mass m and charge q is projected into a region having a perpendicular magnetic field B. Find the angle of deviation fo the particle as it comes out of the magnetic field if the width d of the regions is very smaller then

View SolutionA particle of mass m and charge q is projected into a region having a perpendicular magnetic field B. Find the angle of deviation fo the particle as it comes out of the magnetic field if the width d of the regions is very smaller then

View SolutionA particle of mass and charge is projected into a region having a perpendicular magnetic, field . Find the angle of deviation of the particle as it comes out of the magnetic field if th,, width of the region is (b)
(a) (mv)/(Bq)(mv)/(2 Bq)
View SolutionA particle of mass m and charge q is projected into a region having a perpendicular magnetic, field B . Find the angle of deviation of the particle as it comes out of the magnetic field if the, width of the region is b , which is very slightly less than (mv)/(2Bq)
View SolutionA charge particle of mass m and charge q is projected into a uniform magnetic field of induction b with speed v which is perpendicular to vecB the width of the magnetic field is d the impulse imparted to the particle by the field (dltlt(mv)/qB)) when it comes out of the field zone is
View SolutionA uniform mangetic field of strength B exists in a region of width d. A particle of charge q and mass m is shot perpendicularly (as shown in Fig. ) into the magnetic field. Find the time spent by the particle in the magnetic field if (a) dgt (m u)/(qB) (b) dlt (m u)/(qB)
View SolutionA uniform mangetic field of strength B exists in a region of width d. A particle of charge q and mass m is shot perpendicularly (as shown in Fig. ) into the magnetic field. Find the time spent by the particle in the magnetic field if (a) dgt (m u)/(qB) (b) dlt (m u)/(qB)
View SolutionA uniform mangetic field of strength B exists in a region of width d. A particle of charge q and mass m is shot perpendicularly (as shown in Fig. ) into the magnetic field. Find the time spent by the particle in the magnetic field if (a) dgt (m u)/(qB) (b) dlt (m u)/(qB)
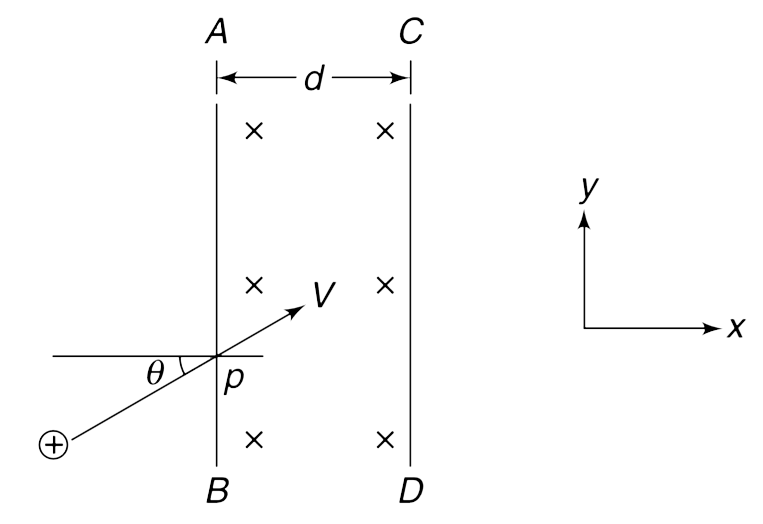
View SolutionAB and CD are two parallel planes perpendicular to the X axis. There is a uniform magnetic field (B) in the space between them directed in negative Z direction. Width of the region having field is d and rest of the space is hav- ing no field. A particle having mass m and charge + q enters the region with a velocity V making an angle q with the X direction as shown.
(a) Find the values of d for which the particle will come out of the magnetic field crossing CD.
(b) For and find the angular deviation in the path of the particle.
(c) Find the deviation in path of the particle if
View SolutionA positive charge q is projected in magnetic field of width (mv)/(sqrt(2)qB) with velocity v as shown in figure. Then time taken by charged particle to emerge from the magnetic field is
View SolutionA charged particle of mass m and charge q is projected into a uniform magnetic field of induciton with speed v which is perpendicular to . The width of the magnetic field is d. The impulse imparted to the particle by the field is
View SolutionA charged particle of mass m and charge q is projected into a uniform magnetic field of induciton with speed v which is perpendicular to . The width of the magnetic field is d. The impulse imparted to the particle by the field is

View SolutionA positive charge q is projected in magnetic field of width (mv)/(sqrt(2)qB) with velocity v . Then, the time taken by charged particle to emerge from the magnetic field is
View SolutionA charge particle of charge 'q' and mass 'm' enters in a given magnetic field 'B' and perpendicular to the magnetic field as shown in the figure. It enters at an angle of 60^(@) with the boundary surface of magnetic field and comes out at an angle of 30^(@) with the boundary surface of the magnetic field as shown in the figure. Find width 'd' in which magnetic field exist.
View SolutionA charge particle of charge 'q' and mass 'm' enters in a given magnetic field 'B' and perpendicular to the magnetic field as shown in the figure. It enters at an angle of 60^(@) with the boundary surface of magnetic field and comes out at an angle of 30^(@) with the boundary surface of the magnetic field as shown in the figure. Find width 'd' in which magnetic field exist.
View SolutionA positively aharged particel (q, m) enters in a uniform magnetic field 'B' at an angle of 60^(@) as shown in figure with speed v_(o) . Collision between the charge particle and the wall is perfectly elastic. Then find the time in which the charge particel comes out from the magnetic field. ("take" d = ((sqrt3 - 1)mv)/(2qB))
View SolutionA positively aharged particel (q, m) enters in a uniform magnetic field 'B' at an angle of 60^(@) as shown in figure with speed v_(o) . Collision between the charge particle and the wall is perfectly elastic. Then find the time in which the charge particel comes out from the magnetic field. ("take" d = ((sqrt3 - 1)mv)/(2qB))
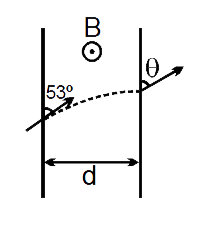
View SolutionA particle moving with velocity v having specific charge (q/m) enters a region of magnetic field B having width at angle to the boundary of magnetic field. Find the angle in the diagram.
View Solution