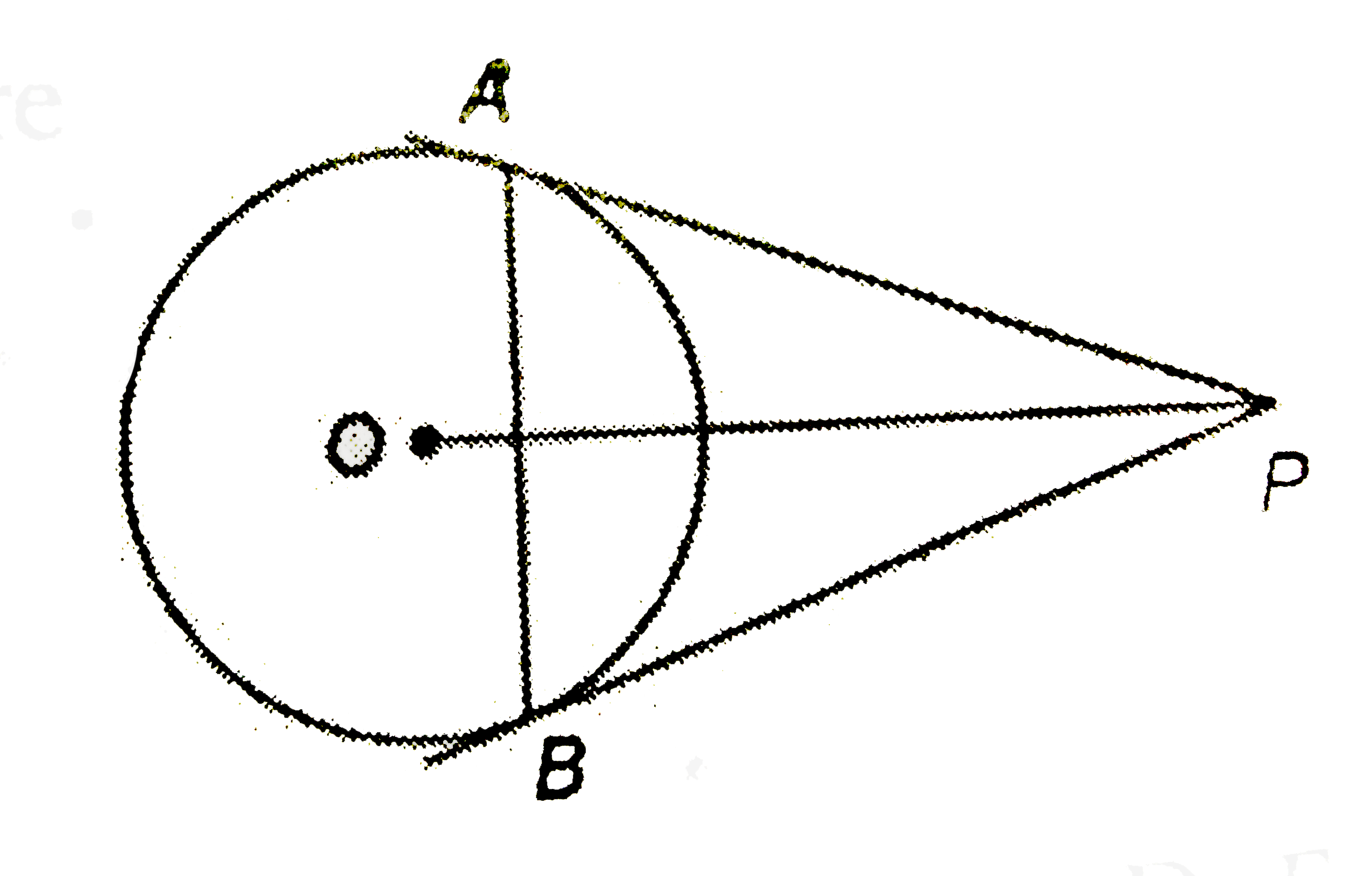
From a point P two tangents PA and PB are drawn to a circle with centre O. If OP is equal to the length of the diameter of the circle then prove that triangle APB is an equilateral triangle.
From the question we have:PA and PB are the tangents to the circle.∴ OA ⊥ PA⇒ ∠OAP = 90°In ΔOPA sin ∠OPA = OA OP = r 2r [Given OP is the diameter of the circle]⇒ sin ∠OPA = 1 2 = sin 30 ⁰⇒ ∠OPA = 30°Similarly it can be proved that ∠OPB = 30°.Now ∠APB = ∠OPA + ∠OPB = 30° + 30° = 60°In ΔPAB PA = PB [length of tangents drawn from an external point to a circle are equal]⇒∠PAB = ∠PBA ............1 [Equal sides have equal angles opposite to them]∠PAB + ∠PBA + ∠APB = 180° [Angle sum property]⇒∠PAB + ∠PAB = 180° – 60° = 120° [Using 1]⇒2∠PAB = 120°⇒∠PAB = 60° .............2From 1 and 2∠PAB = ∠PBA = ∠APB = 60°∴ ΔPAB is an equilateral triangle.
Related Solutions
एक वृत्त C(O, r) पर एक बिन्दु P से दो स्पर्शियाँ PA व PB खींची गयी है । यदि OP = 2r । सिद्ध कीजिए कि एक समबाहु त्रिभुज है।
View SolutionFrom a point , two tangents and are drawn to a circle with centre . If diameter of the circle, show that is equilateral.
View SolutionFrom a point P, two tangents PA and PB are drawn to a circle with centre O. If OP is equal to diameter of the circle, then is
View SolutionFrom a point P two tangents PA and PB are drawn to a circle with centre O.if OP is equal to diameter of the circle then is
View SolutionPA and PB are tangents to a circle with centre O from point P.OP is equal to the diameter of the circle.Prove that ABP is equilateral triangle,
View SolutionFrom a point P, two tangents PA and PB are drawn to a circle with centre O. If OP is equal to diameter of the circle then is___
View Solutionवृत्त के बाहर बिंदु से और दो स्पर्श रेखाएँ खींची गई हैं| दिखाएँ कि यदि , तो समबाहु त्रिभुज हैं|
View SolutionFrom a point P, two tangents PA and PB are drawn to a circle C(0,r). If OP = 2r , show that ∆APB is equilateral.
View SolutionFrom a point P, two tangents PA and PB are drawn to a circle with centre O and radius r. If OP=2r, show that is equilateral.
View SolutionFrom a point P, two tangents PA and PB are drawn to a circle with centre O and radius r. If OP=2r, show that is equilateral.

View SolutionTwo tangents PA and PB are drawn to a circle with centre O from an external point P. Prove that
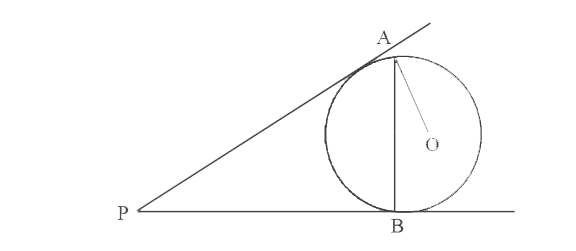
View SolutionFrom a point outside a circle with centre , tangents and are drawn to the circle. Prove that is the right bisector of the line segment .
View Solutionकिसी P बिंदु से, O केंद्र वाले वृत्त पर PA तथा PB को स्पर्श रेखाएं खींची जाती हे| यदि OP वृत्त के व्यास के बराबर हे, तो का मान बताये|
View SolutionPA and PB are tangents to a circle with centre O, from a point P outside the circle and A and B are points on the circle. If , then is equal to
View SolutionTwo tangents PA and PB are drawn to circle with centre O from an external point P. Prove that
View Solutionबिंदु P से वृत पर स्पर्श रेखाऐं PA एवं PB
इस प्रकार खींची गई है की त्रिभुज PAB एक समबाहु त्रिभुज है
तो P का बिन्दुपथ होगा।
View Solutionएक वृत्त C(O, r) के बाह्य बिंदु P से वृत्त पर PA और PB दो स्पर्श रेखाएँ इस प्रकार खींची गई हैं कि है। सिद्ध करो कि
View SolutionFrom an external point two tangents PA and PB are drawn to the circle with center O. Prove that OP is perpendicular bisector of AB.
View SolutionTwo tangent segments PA and PB are drawn to a circle with centre O such that . Prove that OP=2AP.
View SolutionTwo tangent segments and are drawn to a circle with centre such that . Prove that .
View Solution