Two open organ pipe of length L1 and L2 L2>L1 produces x beats /second then speed of sound in organ pipe is
Related Solutions
Questions based on L1-L2
View SolutionQuestions based on L1 and L2
View SolutionIn the figure given below there are two convex lenses L1 and L2 having focal lengths F1 and F2 respectively. The distance between L1 and L2 will be
View SolutionTwo organ (open) pipes of lengths and produce beats/s. Then the speed of sound is nearly
View SolutionIf two open organ pipes of length 50 cm and 51 cm sounded together produce 7 beats per second , the speed of sound is
View SolutionL1 तथा L2 संक्षेप में
View SolutionA closed organ pipe and an open organ pipe of the same length produce four beats, when sounded together. If the length of the closed organ pipe is increased, then the number of beats will
View SolutionWhen two open organ pipes are played together, 5 beats are heard per second. The length of the shorter pipe is 65 cm. Find the length of the second pipe. (speed of sound in air 332.8 ms^(-1) Is.)
View SolutionAt 16^@C , two open organ pipes , when sounded together, produce 34 beats in 2 seconds. How many beats per second will be produced, if the temperature rises to 51^@C ? Neglect the increase in the length of the pipes.
View SolutionAn open organ pipe of length l is sounded together with another open organ pipe of length l + x in their fundamental tones. Speed of sound in air is v . The beat frequency heard will be (x lt lt l) :
View SolutionAn open organ pipe of length l is sounded together with another open organ pipe of length l + x in their fundamental tones. Speed of sound in air is v. the beat frequency heard will be ( x lt lt l )
View SolutionAn open organ pipe of length l is sounded together with another open organ pipe of length l + x in their fundamental tones. Speed of sound in air is v. the beat frequency heard will be ( x lt lt l )
View SolutionConsider two points A and B on L1 and a line L2 as shown in figure. Find the foot of the perpendicular drawn from (2,3,4) on L1 to the line L2.
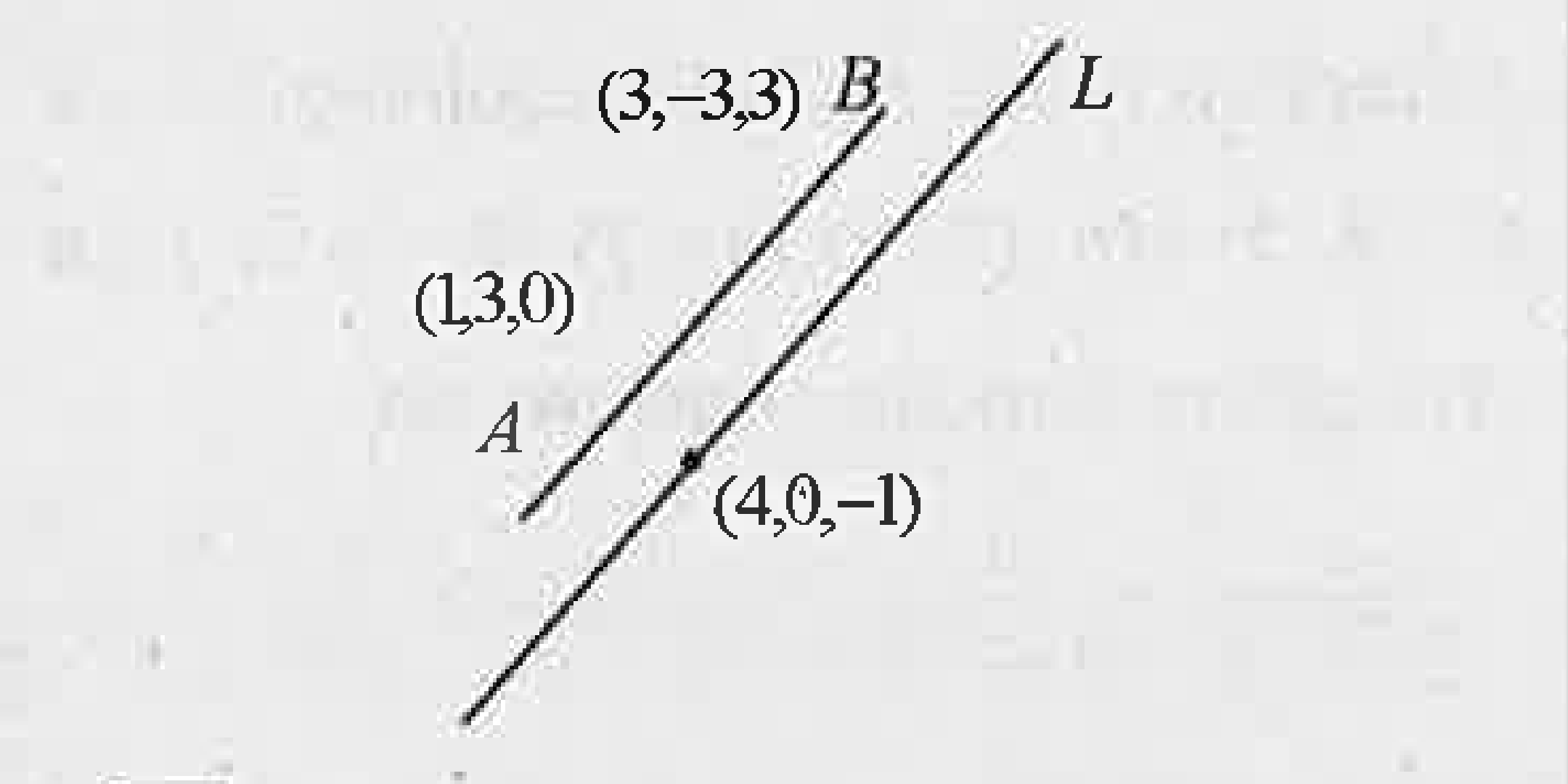
View SolutionA clsoed organ pipe and an open organ pipe of same length produce 2 beats /second while vibrating in their fundamental modes. The length of the open organ pipe is halved and that of closed pipe is doubled . Then the number of beats produced per second while vibrating in the fundamental mode is :
View SolutionA closed organ pipe and an open organ pipe of same length produce 2 beats/second while vibrating in their fundamental modes. The length of the open organ pipe is halved and that of closed pipe is doubled. Then, the number of beats produced per second while vibrating in the fundamental mode is
View SolutionA closed organ pipe and an open organ pipe of same length produce 2 beats/second while vibrating in their fundamental modes. The length of open organ pipe is halved and that of closed pipe is doubled. Then, the number of beats produced per second while vibrating in the fundamental mode is
View SolutionA closed organ pipe and an open organ pipe of same length produce 2 beats/second while vibrating in their fundamental modes. The length of the open organ pipe is halved and that of closed pipe is doubled. Then, the number of beats produced per second while vibrating in the fundamental mode is
View SolutionA closed organ pipe and an open organ pipe of same length produce 2 beats/second while vibrating in their fundamental modes. The length of open organ pipe is halved and that of closed pipe is doubled. Then, the number of beats produced per second while vibrating in the fundamental mode is
View SolutionThe fimdamental frequency of a closed organ pipe is equal to second of an open organ pipe is the length of closed organ pipe is 15 cm. The length of open organ pipe is
View SolutionA closed organ pipe and an open organ pipe when sounded together produce 5 beats/second, if the length of the open pipe is 30 cm, what length of the closed pipe must be changed to bring the two pipes into harmony? [v = 330 m//s]
View Solution