If the equation x3 − 3ax2 + 3bx − c = 0 has positive and distinct roots thenA a2 > b B ab > c C a3 > c D a3 > b2 > c
Correct option A a2 > bLet α β γ be the roots. Then α + β + γ = 3a αβ + βγ + γα = 3b αβγ = c.We have α + β + γ3 > 27 αβγ ⇒ a3 > cAlso
Related Solutions
The correct sequence of electron carriers (Cytochromes) in Respiratory electron transport system is a,a3,b,c and c1 b,c,c1 and a3 b,c1,c,a and a3 a3,a,c,c1 and b
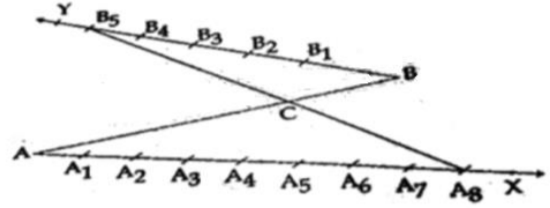
View SolutionIn the figure, if B1, B2, B3,…... and A1,A2, A3,….. have been marked at equal distances. In what ratio C divides AB?
View SolutionIf the equation has positive and distinct roots, then
View SolutionIf the equation has positive and distinct roots, then
View SolutionIf a+b+c=0, then the roots of the equation are
View SolutionIf |(a,b-c,c+b),(a+c,b,c-a),(a-b,b+a,c)| = 0 then equations ax^(2) + bx + c = 0 has a)real and positive roots b)real and negative roots c)imaginary roots d)at least one root positive
View SolutionIf then the roots of the equation where are
View SolutionIf then check the nature of roots of the equation
View SolutionIf (a+b+c)>0 and a < 0 < b < c, then the equation a(x-b)(x-c)+b(x-c)(x-a)+c(x-a)(x-c)=0 has (i) roots are real and distinct (ii) roots are imaginary (iii) product of roots are negative (iv) product of roots are positive
View SolutionIf , then the quadratic equation has
View SolutionThe equation where a, b, c are real and a+b+c = 0 has
View SolutionIf a b c are distinct positive real numbers such that b(a+c)=2ac and given equation is ax^(2)+2bx+c=0 then the roots of the equation are ?
View SolutionIf the roots of the equation then roots of the equation are a b. c. d.
View SolutionIf the roots of the equation then roots of the equation are a b. c. d.
View SolutionIf a+b+c=0, then roots of the equation are
(A) Positive
(B) negative
(C) Real and distinct
(D) imaginary
View SolutionLat be three distinct, positive,numbers such that then the equation has
View SolutionThe order of the differential equation of the family of curves is (where, a, b, c, d, e are arbitrary constants)
View SolutionThe order of the differential equation of the family of curves is (where, a, b, c, d, e are arbitrary constants)
View SolutionLet be the roots of the equation Then the roots of the equation are (b) (d)
View SolutionLet be the roots of the equation Then the roots of the equation are (b) (d)
View Solution