A and B are two separate reservoirs of water. The capacity of A is double that of B. Both the reservoirs are filled completely with water. Water is released simultaneously from both the reservoirs. For each of the reservoirs the rate of flow out at any instant is proportional to the quantity of water left in the reservoir. After 1h the quantity of water in A is 1.5 times the quantity of water in B. After how many hours from the time of release of water do both A and B have the same quantity of water?
Let at time t hours the volume of water in A and B be u and v respectively. From the question du/dt = -k1u 1anddv/dt = -k2v 2At t = 0 u = 2V and v = V from the question. Solving Eq. 1 du/u = -k1dtIntegrating both sides we getlogu = -k1t + c1u = e-k1t + c1 3When t = 0 u = 2V. Then2V = ec1Hence Eq. 3 givesv = Ve-k1t 4Similarly from Eq. 2 we getv = Ve-k2t 5From the question if v = v0 when t = 1 then u = 3/2v0.Therefore Eq. 4 gives3/2v0 = 2Ve-k and Eq. 5 givesV0 = Ve-k2Dividing these we get3/2 = 2e-k1/e-k2 = 2ek2 - k1Thus ek2 - k1 = 3/4 6Let after T hours the volume of water in A and B be equal. Therefore Eqs. 4 and 5 gives2Ve-k1T = Ve-k2T⇒ 2e-k1T = e-k2T ⇒ 2ek2 - k1T = 1Using Eq. 6 we getHence after log4/3 2 hours the reservoirs will have the same quantity of water.
Related Solutions
and are two separate reservoirs of water. Capacity of reservoir is double the capacity of reservoir Both the reservoirs are filled completely with water, their inlets are closed and then the water is released simultaneously from both the reservoirs. The rate of flow of water out of each reservoir at any instant of time is proportional to the quantity of water in the reservoir at the time. One hour after the water is released, the quantity of water is reservoir is times the quantity of water in reservoir After how many hours do both the reservoirs have the same quantity of water?
View Solutionand are two separate reservoirs of water. Capacity of reservoir is double the capacity of reservoir Both the reservoirs are filled completely with water, their inlets are closed and then the water is released simultaneously from both the reservoirs. The rate of flow of water out of each reservoir at any instant of time is proportional to the quantity of water in the reservoir at the time. One hour after the water is released, the quantity of water is reservoir is times the quantity of water in reservoir After how many hours do both the reservoirs have the same quantity of water?
View SolutionA and B are two separate reservoirs of water. Capacity of reservoir A is double the capacity of reservoir Bdot Both the reservoirs are filled completely with water, their inlets are closed and then the water is released simultaneously from both the reservoirs. The rate of flow of water out of each reservoir at any instant of time is proportional to the quantity of water in the reservoir at the time. One hour after the water is released, the quantity of water is reservoir A is 1 1/2 times the quantity of water in reservoir Bdot After how many hours do both the reservoirs have the same quantity of water?
View Solutionand are two separate reservoirs of water. Capacity of reservoir is double the capacity of reservoir Both the reservoirs are filled completely with water, their inlets are closed and then the water is released simultaneously from both the reservoirs. The rate of flow of water out of each reservoir at any instant of time is proportional to the quantity of water in the reservoir at the time. One hour after the water is released, the quantity of water is reservoir is times the quantity of water in reservoir After how many hours do both the reservoirs have the same quantity of water?
View SolutionA तथा Bदो अलग-अलग टैंक है। टैंक A की क्षमता टैंक B की क्षमता की दोगुनी है। दोनों टैंक पानी से पूरे भरे हुए है तथा पानी का प्रवेश बंद कर दिया है। अब दोनों टैंक में से एक साथ पानी निकलता है। किसी भी क्षण पानी के बहने की दर, उस समय टैंक में पानी की मात्रा के समानुपाती होगी। पानी बहने के एक घण्टे पश्चात्, टैंक A में पानी की मात्रा, टैंक B के पानी की मात्रा की 1.5 गुना है। माना तथा टैंक A तथा B की किसी समय t पर पानी के आयतन को दर्शाते है। उपरोक्त जानकारी के आधार पर, निम्न प्रश्न के उत्तर दीजिए:
कितने घण्टों पश्चात् दोनों टैंको में पानी की मात्रा समान होगी
View Solutionएक आयताकार जलाशय में 42000 लीटर पानी है। जलाशय में भरे पानी की गहराई ज्ञात करें यदि जलाशय के आधार की माप 6 मी मी है।
View SolutionA reservoir whose volume is 100 L is filled with brine, which contains 1 kg of disolved salt. the reservoir is fed with water, which enters it at the rate of 3 L/min. This mixture is pumped over the second reservoir whose capacity is also 100 L and which is originally filled with pure water. As a result the surplus quantity of liquid is pouring out of second reservoir. Both the reservoir are kept homogenous at all times. How much salt will the second reservoir have in an hours time?
View Solutionকোনো জলাধারে সঞ্চিত জলের শক্তি হল –
View SolutionWater level in the reservoirs is measured in
View SolutionA rectangular water reservoir contains 42000 litres of water. Find the depth of the water in the reservoir if its base measures 6m by 3.5m.
View SolutionA rectangular water reservoir contains 42,000 litres of water. Find the depth of water in the reservoir, if the base measures 6 by 3.5m.
View SolutionWater is pouring into a cubiodal reservoir at the rate of 60 litres per minute. If the volume of reservoir is find the number of hours it will take to fill the reservoir.
View SolutionWater is pouring into a cubiodal reservoir at the rate of 60 litres per minute. If the volume of reservoir is find the number of hours it will take to fill the reservoir.
View SolutionWater is pouring into a cubiodal reservoir at the rate of 60 litres per minute. If the volume of reservoir is , find the number of hours it will take to fill the reservoir.
View SolutionWater is pouring into a cuboidal reservoir at the rate of 60 litres per minute. If the volume of reservoir is 108 . Find the number of hours it will take to fill the reservoir.
View SolutionWater is pouring into a cubiodal reservoir at the rate of 60 litres per minute. If the volume of reservoir is 108
View SolutionWater is pouring into a cubiodal reservoir at the rate of 60 litres per minute. If the volume of reservoir is , find the number of hours it will take to fill the reservoir.
View SolutionThere are 100 million litres of fluoridated water in the reservoir containing a city\'s water supply, and the water contains 700 kg of fluoride. To decrease the fluoride content, fresh water runs into the reservoir at the rate of 3 million litres per day, and the mixture of water and fluoride, kept uniform, runs-out of the reservoir at the same rate. How many kilograms of fluoride are in the reservoir 60 days after the pure water started to flow into the reservoir?
View SolutionA rectangular water reservoir contains 42000 litres of water. If the length of reservoir is 6 m and its breadth is 3.5 m. The depth of the reservoir is
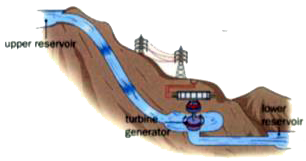
View SolutionWrite the transformation of energy as water flows from the upper reservoir to the turbine generator and from there to the lower reservoir.
View Solution