For a non-zero complex number z let argz denote the principal argument with - π < argz ≤ π. Then which of the following statements is are FALSE? A arg-1 - i = π/4 where i = √-1 B The function f : R → -π π ] defined by ft = arg-1 + it for all t ∈R is continuous at all points of R where i = √-1C For any two non-zero complex numbers z1 and z2 argz1/z2 - argz1 + argz2 is an integer multiple of 2π D For any three given distinct complex numbers z1 z2 and z3 the locus of the point z satisfying the condition argz -z1z2 - z3/z - z3z2 - z1 = π lies on a straight line
Answer A B DsolutionDiscontinuous at t = 0.=> z z1 z2 z3 are concyclic.
Related Solutions
Extend the definition of the following by continuity at the pointx=π
View SolutionLet z and w be two non-zero complex numbers such that ∣z∣=∣w∣ and arg(z)+arg(w)=π, then z equals
View SolutionSimplify: where
View SolutionEvaluate : . a) b) c) d)
View SolutionTwo angles of a triangle are 3 . Then the third angle is (i) 3π/4 (iii) π/3
View SolutionFor a non-zero complex number , let denote the principal argument with Then, which of the following statement(s) is (are) FALSE? where (b) The function defined by for all , is continuous at all points of , where (c) For any two non-zero complex numbers and , is an integer multiple of (d) For any three given distinct complex numbers , and , the locus of the point satisfying the condition , lies on a straight line
View SolutionFor a non-zero complex number , let denote the principal argument with Then, which of the following statement(s) is (are) FALSE? where (b) The function defined by for all , is continuous at all points of , where (c) For any two non-zero complex numbers and , is an integer multiple of (d) For any three given distinct complex numbers , and , the locus of the point satisfying the condition , lies on a straight line
View SolutionThe roots of the equation cos ^7x+sin^4x=1 in the interval (−π,π) are
View SolutionEvaluate : for
View SolutionA uniform magnetic field is restricted within a region of radius r. The magnetic field changes with time at a rate . Loop 1 of radius R r encloses the region r and loop 2 of radius R is outside the region of magnetic field as shown in figure. Then, the emf generated is
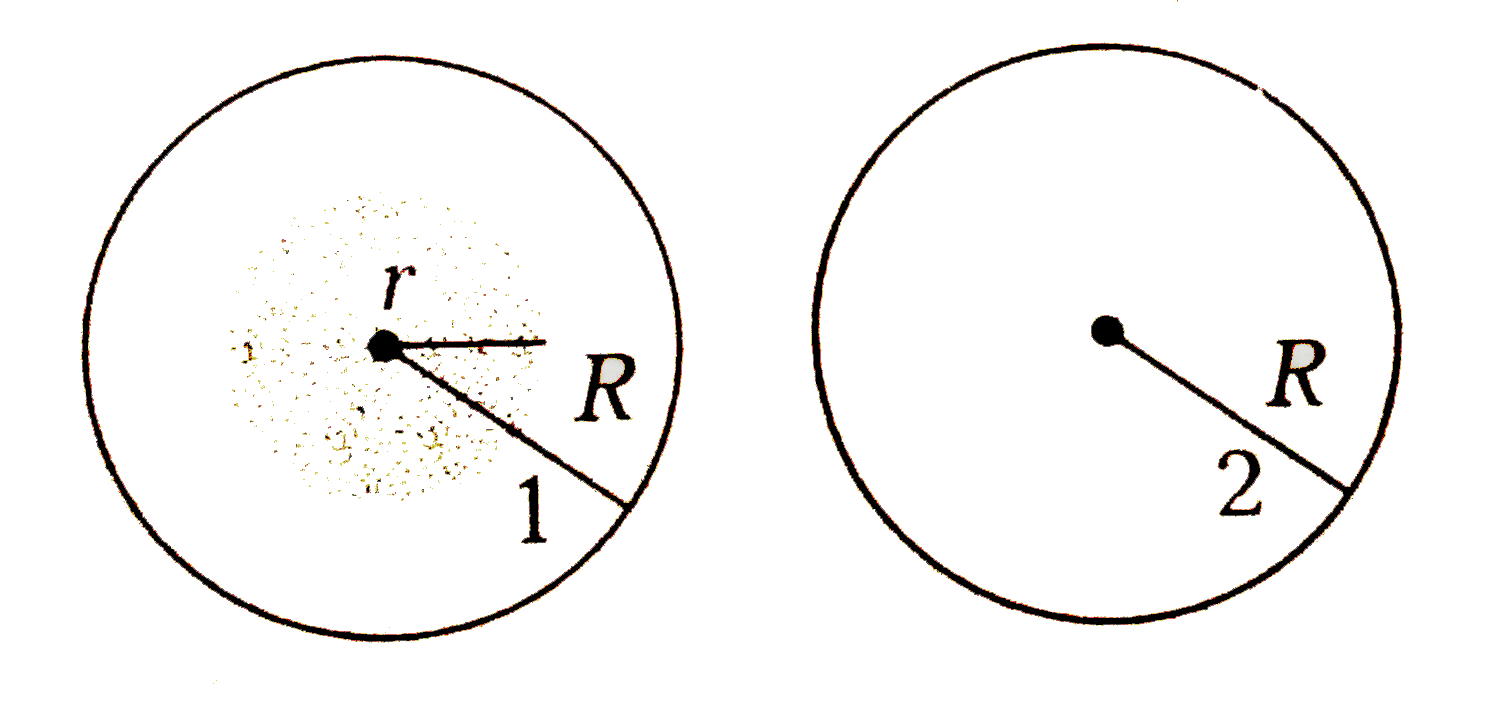
Zero in loop 1 and zero in loop 2
− d B d t π r 2 in loop 1 and − d B d t π 2 in loop 2
− d B d t π R 2 in loop 1 and zero in loop 2
− d B d t π r 2 in loop 1 and zero in loop 2
View SolutionThe number of ordered pairs (α,β), where α,β∈(−π,π) satisfying cos (α−β)=1 and cos(α+β)=1/e is
View SolutionThe number of ordered pairs (α,β), where α,β∈(−π,π) satisfying cos (α−β)=1 and cos(α+β)=1/e is
View SolutionIf cos(α−β)=1 and cos(α+β)= 1/e , where α, β∈[−π,π]. Then number of ordered pairs of (α,β) is
View SolutionThe number ‘π’ is
View SolutionThe number ‘π’ is
View SolutionThe number ‘π’ is
View SolutionSynergic Bonding in NO/PCl3/H2 || Synergic Bonding in π-doner Ligands || List OF all imp π-doner/π* acceptor Ligand and their Representation || Hapticity
View SolutionSimplify tan^-1[3sin2α/(5+3 cos〖2 α〗 )] + tan-1[tanα/4] , where -π/2<α<π/2.
View SolutionThe range of F(X) = Cos [X], Where − π/ 2 < X < π/ 2 . is
View SolutionLet the function f(x) be defined as follows:(x)= , then which of the following statement(s) is/are correct
View Solution