In a cyclic quadrilateral ABCD prove that tan^2B/2 = s - as - b/s - cs - d a b c and d being the lengths of sides AB BC CD and DA respectively and ‘s’ is semi-perimeter of quadrilateral.
See Fig. In DABCAC2 = a2 + b2 − 2ab cos B ....1In ΔADCAC2 = c2 + d2 − 2cd cos D= c2 + d2 − 2cd cos 180° − B= c2 + d2 + 2cd cos B ......2From Eqs. 1 and 2 we get
Related Solutions
In a cyclic quadrilateral ABCD, prove that being the lengths of sides ABC, CD and DA respectively and s is semi-perimeter of quadrilateral.
View SolutionIn a cyclic quadrilateral ABCD, prove that being the lengths of sides ABC, CD and DA respectively and s is semi-perimeter of quadrilateral.
View SolutionIn a cyclic quadrilateral ABCD, prove that being the lengths of sides ABC, CD and DA respectively and s is semi-perimeter of quadrilateral.
View SolutionThe area of any cyclic quadrilateral ABCD is given by , where 28 = a + b + c + d, a, b,c and d are the sides of the quadrilateral. Now consier a cyclic quadrilateral ABCD of area 1sq.unit and answer the following questions:
The minimum perimeter of the quadrilateral is
View SolutionThe area of any cyclic quadrilateral ABCD is given by , where are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
The minium perimeter of the quadrilateral is
View SolutionThe area of any cyclic quadrilateral ABCD is given by , where 28 = a + b + c + d, a, b,c and d are the sides of the quadrilateral. Now consier a cyclic quadrilateral ABCD of area 1sq.unit and answer the following questions:
When the perimeter is minimum, the quadrilateral is necessarily
View SolutionThe area of any cyclic quadrilateral ABCD is given by , where are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
The minium perimeter of the quadrilateral is
View SolutionThe area of any cyclic quadrilateral ABCD is given by , where are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
The minium perimeter of the quadrilateral is
View SolutionThe area of any cyclic quadrilateral ABCD is given by , where are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
The minium perimeter of the quadrilateral is
View SolutionThe area of any cyclic quadrilateral ABCD is given by , where 28 = a + b + c + d, a, b,c and d are the sides of the quadrilateral. Now consier a cyclic quadrilateral ABCD of area 1sq.unit and answer the following questions:
The minimum value of the sum of the lengths of diagonals
View Solutionis a quadrilateral; are the points of trisection of side respectively and are adjacent to ; prove that is parallelogram.
View Solutionएक वृत्त, एक चतुर्भुज ABCD की चारों भुजाओं को अन्तः स्पर्श करता है। सिद्ध कीजिए कि-
AB + CD = AD + BC.
(अथवा) आकृति, में एक चतुर्भुज ABCD, O केन्द्र वाले वृत्त के परिगत इस प्रकार बनाई गई है कि भुजाएँ AB, BC, CD, तथा DA वृत्त को क्रमशः बिन्दुओं P, Q, R तथा S पर स्पर्श करती हैं। सिद्ध कीजिए कि
AB + CD = BC + DA
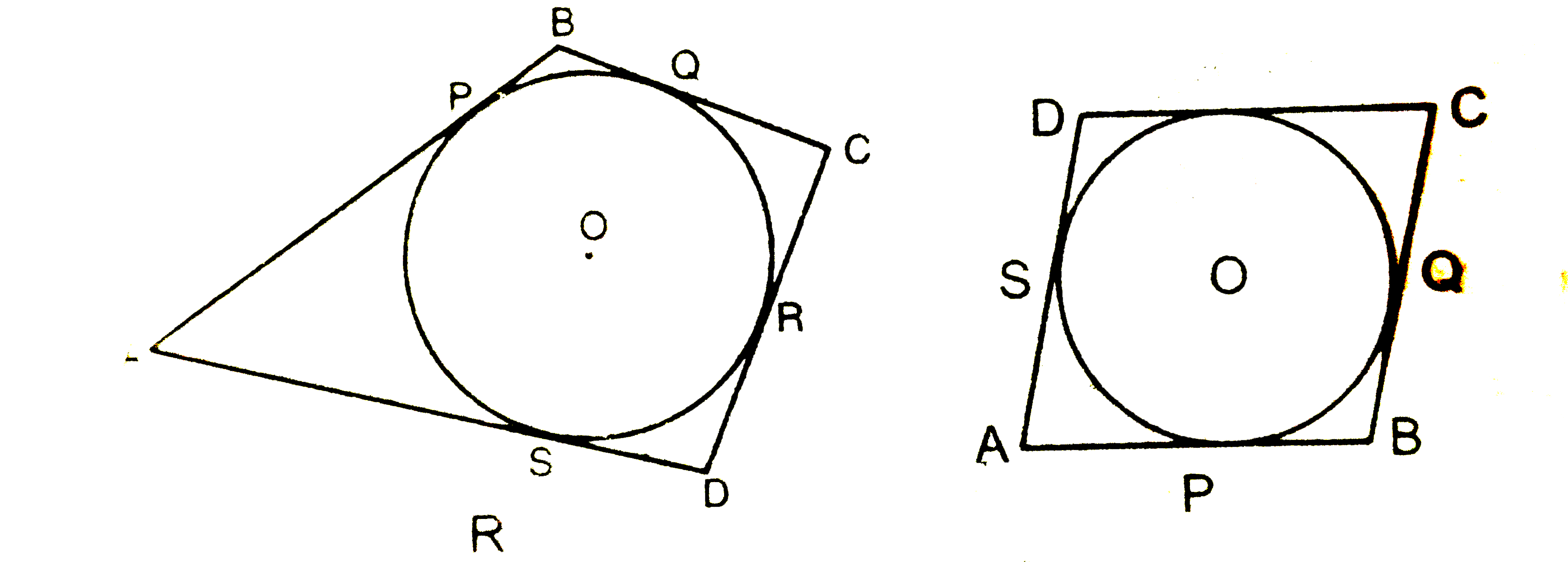
View SolutionIn Fig.2, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
View SolutionIn Fig.2, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
View SolutionABCD ਇੱਕ ਆਇਤ ਹੈ, ਜਿਸ ਵਿਚ P, Q, R ਅਤੇ S ਅਤੇ ਕ੍ਰਮਵਾਰ ਭੁਜਾਵਾਂ AB, BC, CD ਅਤੇ DA ਦੇ ਮੱਧ ਬਿੰਦੂ ਹਨ। ਦਰਸਾਉ ਕਿ ਚਤੁਰਭੁਜ PQRS ਇੱਕ ਸਮਚਤੁਰਭੁਜ ਹੈ।
View SolutionP, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View SolutionP, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View SolutionP,Q,R and S are respectively the mid points of the sides AB,BC,CD and DA of a quadrilateral ABCD such that ACbotBD . Prove that PQRs is a rectangle.
View SolutionABCD is a rectangle and P,R and S are the mid - points of the AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionIf ABCD is a rectangle and P, Q, R, S are the midpoints of AB BC CD and DA respectively, then the area of the quadrilateral PQRS is equal to
View Solution