A horizontal rod rotates about a vertical axis through one end. A ring which can slide along the rod without friction is initially close to the axis and then slides to the other end of the rod. In this process which of the following quantities will be conserved? [L = angular momentum ET = total kinetic energy ER = rotational kinetic energy.] a L only b L and ET only c L and ER only d ET only
Correct Answer is: b L and ET only As no external torque acts on the system its angular momentum is conserved. Since there is no loss of energy due to friction the total energy is conserved. However the ring acquires some translational kinetic energy as it slides outwards and hence rotational kinetic energy is not conserved.
Related Solutions
A horizontal rod rotates about a vertical axis through one end. A ring, which can slide along the rod witgour friction, is initially close to the axis and then slides to the other end of the rod. In this process, which of the following quantities will be conserved? {L = angular momentum, E_(T) = total kinetic energy, E_(R) = rotational kientic energy.]
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:
View Solutionएक छड़ अपनी लम्बाई के अभिलम्ब उसके एक सिरे से पारित अक्ष के परितः 50 घूर्णन प्रति मिनट की दर से घुमायी जाती है। छड़ की घूर्णन गतिज ऊर्जा 400 जूल है। छड़ का जड़त्व आघूर्ण ज्ञात कीजिए।
View SolutionA rod of mass and length is connected with a light rod of length . The composite rod is made to rotate with angular velocity as shown in the figure. Find the
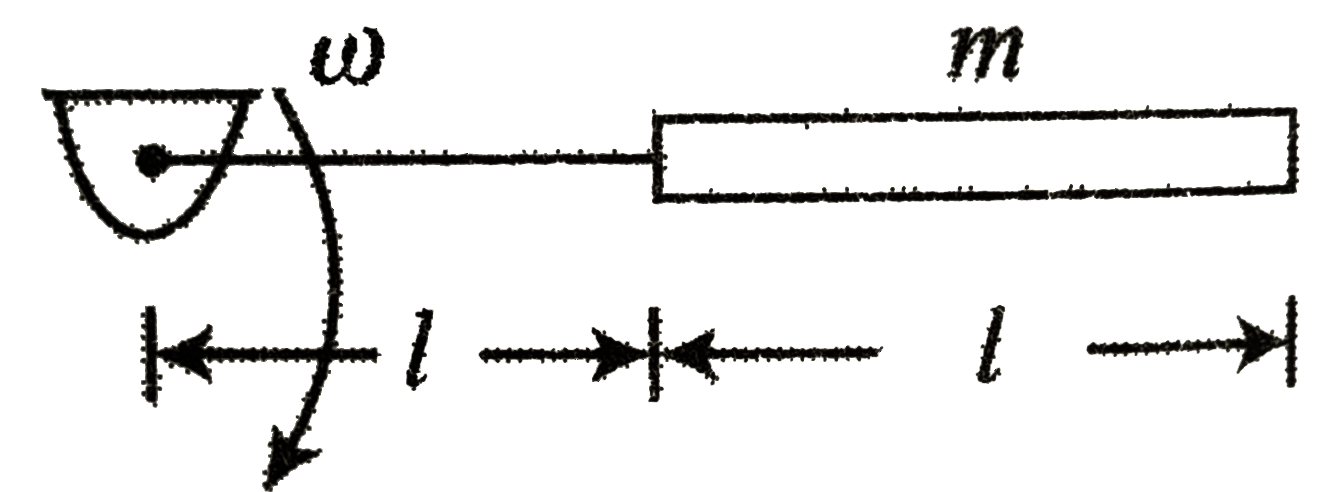
a. translational kinetic energy.
b. rotational kinetic energy.
c. total kinetic energy of rod.
View SolutionA rod of mass m and length l is connected with a light rod of length l . The composite rod is made to rotate with angular velocity omega as shown in the figure. Find the a. translational kinetic energy. b. rotational kinetic energy. c. total kinetic energy of rod.
View SolutionA uniform rod of mass 300 g and length 50 cm rotates at a uniform angular speed of 2 rad/s about an axis perpendicular to the rod through an end. Calculate a. the angular momentum of the rod about the axis of rotation b. the speed of the centre of the rod and c. its kinetic energy.
View SolutionA uniform thin rod of length l is suspended from one of its ends and is rotated at f rotations per second. The rotational kinetic energy of the rod will be
View SolutionA uniform thin rod of length l is suspended from one of its ends and is rotated at f rotations per second. The rotational kinetic energy of the rod will be
View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed in the horizontal plane then the angular momentum of the rod about the axis is:
View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed in the horizontal plane then the angular momentum of the rod about the axis is:
View SolutionA uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle theta with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:
View SolutionA mechanism consists of a part which is translated with a velocity u and a rod AB of length L and mass M hinged at A The rod rotates about axis A with angular velocity omega the kinetic energy of rod when it is vertical as shown is
View SolutionA horizontal rod of length 'l' rotates about a vertical axis with a uniform angular velocity 'omega' . A uniform magnetic field of induction B exists parallel to the axis of rotation. The potential different between the ends of the rod is
View SolutionA uniform rod of mass 300 g and length 50 cm rotates at a uniform asngulr speed of 2 rad/s about an axis perpendicular to the rod through an end. Calculte a. the angular momentum of the rod about the axis of rotation b. the speed of thecentre of the rod and c. its kinetic energy.
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity omega about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity omega about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA uniform rod of mass and length rotates in a horizontal plane with an angular velocity about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View Solutionl लम्बाई की एक छड़ कब्जे पर अपने एक क्षैतिजतः सिरे पर घूमती है। यह गिरने के लिए स्वतन्त्र है। छड़ के दूसरे सिरे का वेग है
View SolutionA rod PQ of length L revolves in a horizontal plane about the axis YY´. The angular velocity of the rod is w. If A is the area of cross-section of the rod and r be its density, its rotational kinetic energy is
View Solution