Let fx = 2 + cosx for all real x.Statement-1: For each real t there exists a point c in [t t + π] such that f′c = 0. BecauseStatement-2: ft = ft + 2π for each real t.A Statement-1 is True Statement-2 is True; Statement-2 is a correct explanation for Statement-1B Statement-1 is True Statement-2 is True Statement-2 is NOT a correct explanation for Statement-1C Statement-1 is True Statement-2 is FalseD Statement-1 is False Statement-2 is True
Answer is B Statement-1 is True Statement-2 is True Statement-2 is NOT a correct explanation for Statement-1We have fx = 2 + cosx for all values of x.f′x = -sinxStatement-1:f′t = -sintf′π + t = sintAlso sincef′t · f′π + t = -sin2twhich is negative the equation f′t = 0 has at least one solution in [t t + π].Statement-2: Since fx = 2 + cosx is a periodic function with period 2π we getf2π + t = ft
Related Solutions
Statement 1 is True: Statement 2 is True; Statement 2 is a correct explanation for statement 1 Statement 1 is true, Statement 2 is true;2 Statement 2 not a correct explanation for statement 1. Statement 1 is true, statement 2 is false Statement 1 is false, statement 2 is true Statement I: If is obtuse angle I then because Statement II: In a. b. c. d.
View SolutionStatement 1 is True: Statement 2 is True; Statement 2 is a correct explanation for statement 1 Statement 1 is true, Statement 2 is true;2 Statement 2 not a correct explanation for statement 1. Statement 1 is true, statement 2 is false Statement 1 is false, statement 2 is true Statement I: If is obtuse angle I then because Statement II: In a. b. c. d.
View SolutionStatement 1. for all real , Statement 2. For positive numbers, (A) Both Statement 1 and Statement 2 are true and Statement 2 is the correct explanation of Statement 1 (B) Both Statement 1 and Statement 2 are true and Statement 2 is not the correct explanation of Statement 1 (C) Statement 1 is true but Statement 2 is false. (D) Statement 1 is false but Statement 2 is true
View SolutionStatement 1. for all real , Statement 2. For positive numbers, (A) Both Statement 1 and Statement 2 are true and Statement 2 is the correct explanation of Statement 1 (B) Both Statement 1 and Statement 2 are true and Statement 2 is not the correct explanation of Statement 1 (C) Statement 1 is true but Statement 2 is false. (D) Statement 1 is false but Statement 2 is true
View SolutionLet F(x) be an indefinite integral of sin^(2)x Statement-1: The function F(x) satisfies F(x+pi)=F(x) for all real x. because Statement-2: sin^(2)(x+pi)=sin^(2)x for all real x. A) Statement-1: True , statement-2 is true,statement-2 is correct explanation for statement-1 (b) statement-1 true, statement-2 true and Statement -2 is not a correct explanation for statement -1 c) Statement-1 is True, Statement -2 is False. D) Statement-1 is False, Statement-2 is True.
View SolutionStatement 1 is True: Statement 2 is True; Statement 2 is a correct explanation for statement 1 Statement 1 is true, Statement 2 is true;2 Statement 2 not a correct explanation for statement 1. Statement 1 is true, statement 2 is false Statement 1 is false, statement 2 is true Statement I: Statement II: a. b. c. d.
View SolutionSTATEMENT 1: int_0^(pi/4)log(1+t a ntheta)d theta=pi/8log2. STATEMENT 2: int_0^(pi/2)logsin theta d theta =-pilog2. (a) statement 1 is true, statement 2 is true, Statement 2 is the correct explanation for statement 1. (b) statement 1 is true, statement 2 is true, Statement 2 is not correct explanation for statement 1. (c) statement 1 is true, statement 2 is not true. (d) statement 2 is true, statement 1 is not true.
View SolutionStatement I: If
Statement II:
Statement 1 is True: Statement 2 is True, Statement 2 is a correct explanation for statement 1.
Statement 1 is true, Statement 2 is true;2 Statement 2 not a correct explanation for statement 1.
Statement 1 is true, statement 2 is false.
Statement 1 is false, statement 2 is true
View SolutionLet F(x) be an indefinite integral of
Statement-1: The function F(x) satisfies for all real x. because
Statement-2: for all real x.
A) Statement-1: True , statement-2 is true, Statement -2 is not a correct explanation for statement -1
c) Statement-1 is True, Statement -2 is False.
D) Statement-1 is False, Statement-2 is True.
View SolutionLet F(x) be an indefinite integral of
Statement-1: The function F(x) satisfies for all real x. because
Statement-2: for all real x.
A) Statement-1: True , statement-2 is true, Statement -2 is not a correct explanation for statement -1
c) Statement-1 is True, Statement -2 is False.
D) Statement-1 is False, Statement-2 is True.
View SolutionStatement 1: does not exist (where {.} denotes fractional part function). Statement 2: is discontinuous at (a)Statement 1 is True: Statement 2 is True; Statement 2 is a correct explanation for statement 1 (b)Statement 1 is true, Statement 2 is true; Statement 2 not a correct explanation for statement 1. (c)Statement 1 is true, statement 2 is false (d)Statement 1 is false, statement 2 is true
View SolutionStatement 1: If does not exist. Statement 2: can be rational or irrational value. Statement 1 is True: Statement 2 is True; Statement 2 is a correct explanation for statement 1 Statement 1 is true, Statement 2 is true; Statement 2 not a correct explanation for statement 1. Statement 1 is true, statement 2 is false Statement 1 is false, statement 2 is true
View SolutionStatement-1: In naphthalene all C-C bonds are equal
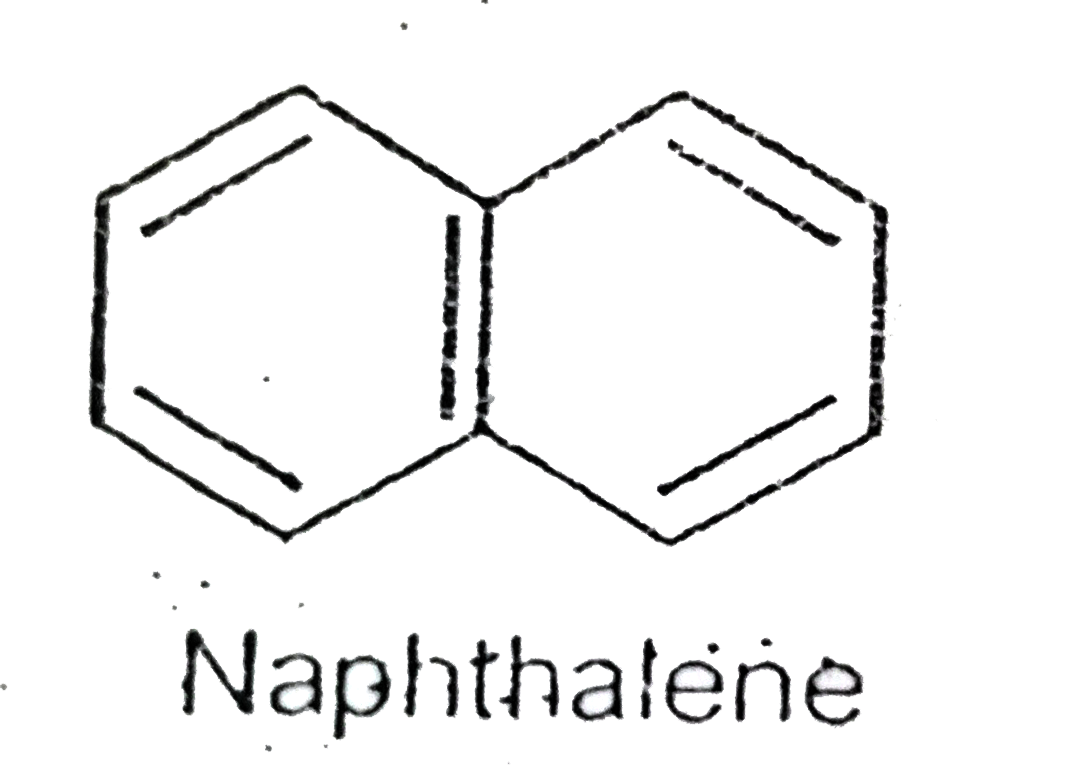
and
Statement-2: Like benzene naphthalene is also aromatic.
(a) Statement-1 is true, Statement-2 is true, Statement-2 is a correct explanation for Statement-1
(b) Statement-1 is true, Statement-2 is true, Statement-2 is not a correct explanation for Statement -1
(c) Statement -1 is true, Statement -2 is false
(d) Statement -1 is false, Statement -2 is true
View SolutionStatement-1: The function satisfies ,Statement-2: (A) Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1. (B) Statement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1. (C) Statement-1 is True, Statement-2 is False. (D) Statement-1 is False, Statement-2 is True.
View SolutionStatement-1: The function satisfies ,Statement-2: (A) Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1. (B) Statement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1. (C) Statement-1 is True, Statement-2 is False. (D) Statement-1 is False, Statement-2 is True.
View Solution9, Let A be a 2 x 2 matrix with real entries. Let I be the 2 × 2 2identity matrix. Denote by tr (A), the sum of diagonal entries of A. Assume that A2 -1 nvo bud o malai Statement 1: If A 1 and A?-1, then det A =-1. Statement 2: If A 1 and A?-I, then tr (A)?0 A. Statement 1 is false, statement 2 is true. B. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1 . C. Statement 1 is true, statement 2 is true; statement 2 is nota correct explanation for statement 1. D. Statement 1 is true, statement 2 is false.
View Solutionमाना सभी वास्तविक के लिए
कथन - 1 : सभी वास्तविक के लिए में एक बिन्दु इस प्रकार है कि क्योंकि
कथन - 2 : प्रत्येक वास्तविक के लिए
View SolutionStatement 1: The function is discontinuous at all integers. Statement 2: is discontinuous at all integral values of Statement 1 is True: Statement 2 is True; Statement 2 is a correct explanation for statement 1 Statement 1 is true, Statement 2 is true; Statement 2 not a correct explanation for statement 1. Statement 1 is true, statement 2 is false Statement 1 is false, statement 2 is true
View SolutionStatement 1 is True: Statement 2 is True; Statement 2 is a correct explanation for statement 1 Statement 1 is true, Statement 2 is true;2 Statement 2 not a correct explanation for statement 1. Statement 1 is true, statement 2 is false Statement 1 is false, statement 2 is true Statement I: is positive for all real values of oly when because Statement II: a. b. c. d.
View SolutionLet A be a matrix
Statement -1 adj
Statement-2 . Select the correct alternative: a) Statement -1 is true , Statement -2 is true , Statement -2 is a correct explanation for Statement -1 b) Statement -1 is true , Statement -2 is true, Statement -2 is not a correct explanation for Statement -1 c) Statement-1 is true , Statement -2 is false d) Statement -1 is false , Statement -2 is true
View Solution