If a2 + b2 + c2 = 1 prove that |a2 + b2 + c2cosϕ ab1 - cosϕ ac1 - cosϕ ba1 - cosϕ b2 + c + a2cosϕ bc1 - cosϕ ca1 - cosϕ cb1 - cosϕ c2 + a2 + b2cosϕ| is independent of a b and c.
Multiplying C1 C2 C3 by a b c respectively and taking a b c common from R1 R2 R3 respectively we get Taking a2 + b2 + c2 common from C1 we get= a2 + b2 + c22 cos2ϕ {by property since all elements are zero below leading diagonal}= 12 cos2ϕ = cos2ϕ which is independent of a b and c.
Related Solutions
If the angles A,B,C of a triangle are in A.P.and sides a,b,c are in G.P. ,then a2,b2,c2 are in
View SolutionIf the determinant ∣ cos(θ+ϕ) sinθ −cosθ −sin(θ+ϕ) cosθ sinθ cos2ϕ sinϕ cosϕ ∣ is positive is independent of theta is independent of varphi none of these
View SolutionDiscussion OF Ex-9.4 (Optional)|| Important Result a2=b2+c2(PythagorasTheorem) ||Chapter summary
View Solutionসংখ্যারেখা তৈরি করে নীচের সংখ্যাগুলিকে সংখ্যারেখায় দেখাও ও নাম দাও। +5, -2, +3, -6, +2, -5, -এ যথাক্রমে A,B,C,D,E ও F নাম দাও। B থেকে E-এর দূরত্ব কত ঘর মেপে দেখো।
View SolutionIf the equation of the locus of a point equidistant from the points (a_1, b_1) and (a_2, b_2) is (a_1-a_2)x+(b_1-b_2)y+c=0 , then the value of c is a a2-a2 2+b1 2-b2 2 sqrt(a1 2+b1 2-a2 2-b2 2) 1/2(a1 2+a2 2+b1 2+b2 2) 1/2(a2 2+b2 2-a1 2-b1 2)
View SolutionIf the equation of the locus of a point equidistant from the points and is , then the value of is
View SolutionLet be a binary operation on the set Q of rational numbers as follows: find is it associative?
View SolutionA(a1, b1) மற்றும் B(a2, b2) ஆகிய புள்ளிகளை இணைக்கும் கோட்டுத் துண்டை X-அச்சு எந்த விகிதத்தில் பிரிக்கும்?
View SolutionLet be a binary operation on the set Q of rational numbers as follows: find is it commutative?
View SolutionThe ratios a1/a2 , b1/b2 , c1/c2 Find out whether the given linear equations are pairwise compatible or incompatible: 2x - 3y = 8 and 4x - 6y = 9.
View SolutionMolecular Orbital Diagram Of B2, C2 ,N2 |S-P Mixing
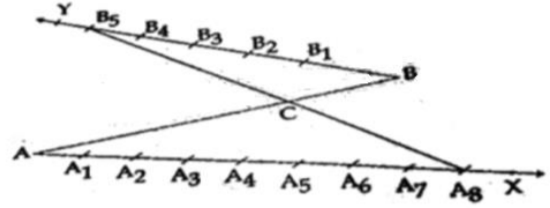
View SolutionIn the figure, if B1, B2, B3,…... and A1,A2, A3,….. have been marked at equal distances. In what ratio C divides AB?
View SolutionIf x = a cos θ and y = b sin θ, then b2x2 + a2y2 = …………… (1) a2b2 (2) ab (3) a4b4 (4) a2 + b2
View SolutionSuppose a set of rational numbers Q Defined below ** One of the two-dimensional processes is: a**b=a2-b2 Find out if this is a companion.
View SolutionSuppose a set of rational numbers Q Defined below ** One of the two-dimensional processes is: a**b=a2-b2 Find out if this is a rotation.
View SolutionLet θ, ϕ ∈ [0, 2] be such that 2cosθ(1 - sinϕ) = sin2θ(tan2θ(tan(θ/2) + cot(θ/2))cosϕ - 1, tan(2π - θ) > 0 and - 1 < sinθ < - √3/2. Then ϕ cannot satisfy
View Solution35. If the sum of the roots of be equal to sum of the squares, then- (A) 2ac = ab + b2 (B) 2ab-bc + c2 c (D) None of these (D) None of these (C) 2bc -ac+2
View Solution
View Solutionவைட்டமின்கள் B2 ஆனது _____ எனவும் அறியப்படுகிறது.
View SolutionVitamins B2 is also known as _____.
View Solution