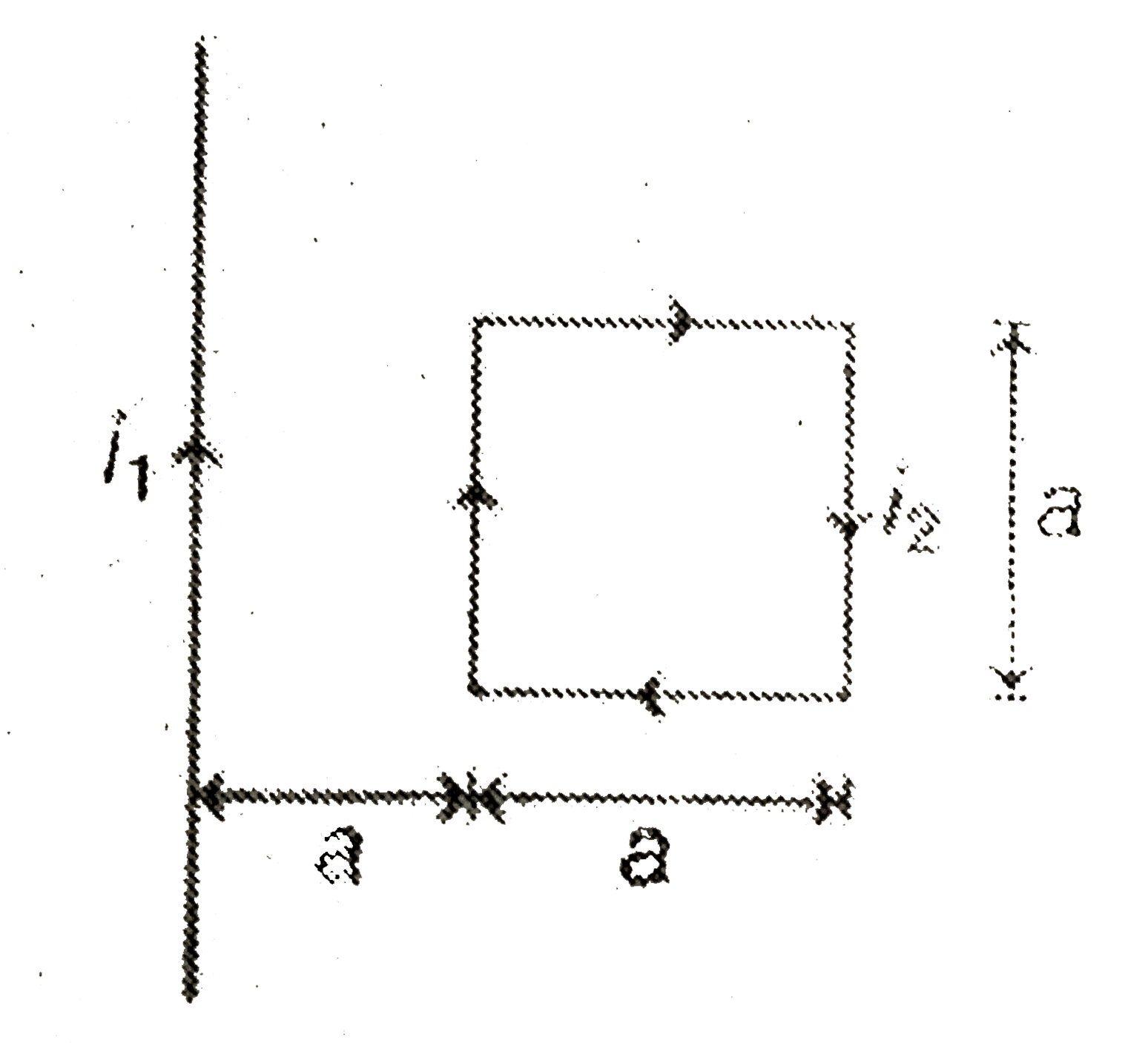
a Define the term “self-inductance” of a coil. Wire its SI unit. b A rectangular loop of sides a and b carrying current I2 is kept at a distance a from an infinity long straight wire carrying current I1 as shown in the figure. Obtain an expression for the resultant force acting on the loop.
a Self-inductance of a coil is equal to emf induced in coil when the rate of change of current through coil is unity or it is equal the amount of magnetic flux linked with coil when unit current flow through the coil. If current I is flowing through coil in time t and ϕ is the flux linked with coil thenϕ ∝ I ⇒ ϕ = LIwhere L is self-inductance for unit current that is I = 1 and L =ϕ.The SI unit of self-inductance is henry H.b Let PQRS be the rectangular loop of side a and b.It is placed at distance a from infinite long straight wire AB. • Current through PQRS = I2.• Current through AB = I1.• Current through the arm PQ is in same direction as current through the arm AB so they attract each other. • Current through the arm RS is in opposite direction as current through the arm AB so they repel each other. • Also the force on arm QR and SP is equal and opposite and hence it will cancel each other.Now we know the magnetic force between two parallel current-carrying conductor of length L iswhere r is the distance between two conductors and L is the length of the conductor. Thus the force on arm PQ is given asForce on arm RS is given asThus the resultant force acting on the loop isThis is the resultant force acting on the loop.
Related Solutions
Define mutual inductance and write its SI unit. A square loop of side 'a' carrying a current I_2 is kept at distance x from an infinitely long straight wire carrying a current I_1 as shown in the figure SAQ 41. Obtain the expression for the resultant force acting on the loop.
View SolutionAnswer the following:
(a) Define mutual inductance and write its S.I. unit.
(b) A square loop of side carrying a current is kept at distance from an infinitely long straight wire carrying a current as shown in the figure. Obtain the expression for the resultant force on the loop.

View SolutionA rectangular loop of wire of size carries a steady current of 2A. A straight long wire carrying 5 A current is kept near the loop as shown. If the loop and the wire are coplanar, find
(i) the torque acting on the loop and
(ii) the magnitude and direction of the force on the loop due to the current carrying wire.
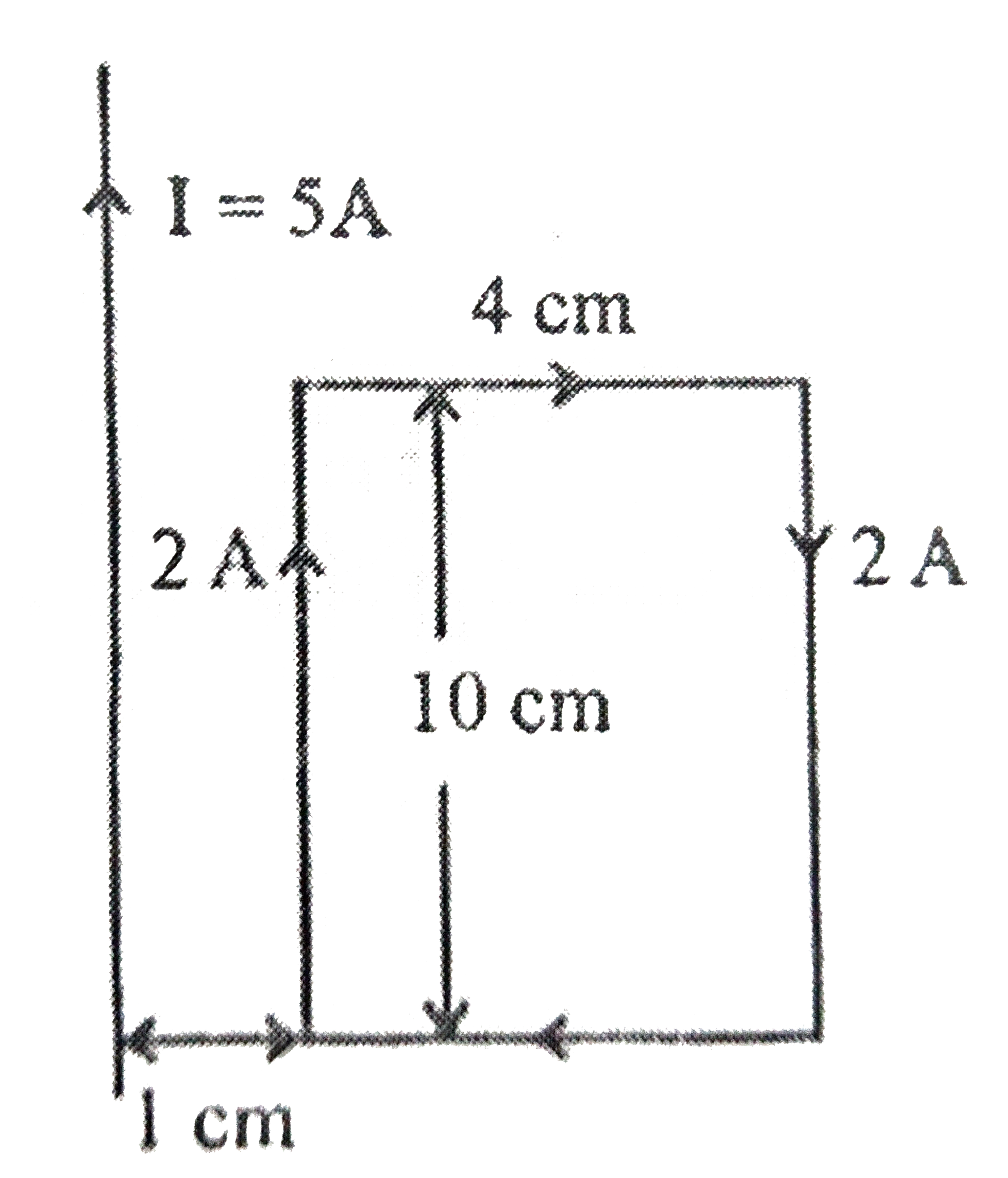
View SolutionA rectangular loop of wire of size 4 cm xx 10 cm carries a steady current of 2A. A straight long wire carrying 5 A current is kept near the loop as shown. If the loop and the wire are coplanar, find (i) the torque acting on the loop and (ii) the magnitude and direction of the force on the loop due to the current carrying wire.
View SolutionA rectangular loop of wire of size 2.5 cm xx 4 cm carries a steady current of 1A. A straight long wire carrying 2 A current is kept near the loop as shown. If the loop and the wire are coplanar, find (i) the torque acting on the loop and (ii) the magnitude and direction of the force on the loop due to the current carrying wire.
View SolutionA rectangular loop of wire of size 2.5 cm xx 4 cm carries a steady current of 1A. A straight long wire carrying 2 A current is kept near the loop as shown. If the loop and the wire are coplanar, find (i) the torque acting on the loop and (ii) the magnitude and direction of the force on the loop due to the current carrying wire.
View SolutionA rectangular loop carrying a current i_(2) situated near a long straight wire carrying a steady current i_(1) . The wire is parallel to one of the sides of the loop and is in the plane of the loop as shown in the figure. Then the current loop will
View SolutionA rectangular loop carrying a current i_(2) situated near a long straight wire carrying a steady current i_(1) . The wire is parallel to one of the sides of the loop and is in the plane of the loop as shown in the figure. Then the current loop will
View SolutionA rectangular loop of wire of size carries a steady current of 1A. A straight long wire carrying 4 A current is kept near the loop as shown. If the loop and the wire are coplanar, find
(i) the torque acting on the end
(ii) the magnitude and direction of the force on the loop due to the current carrying wire.
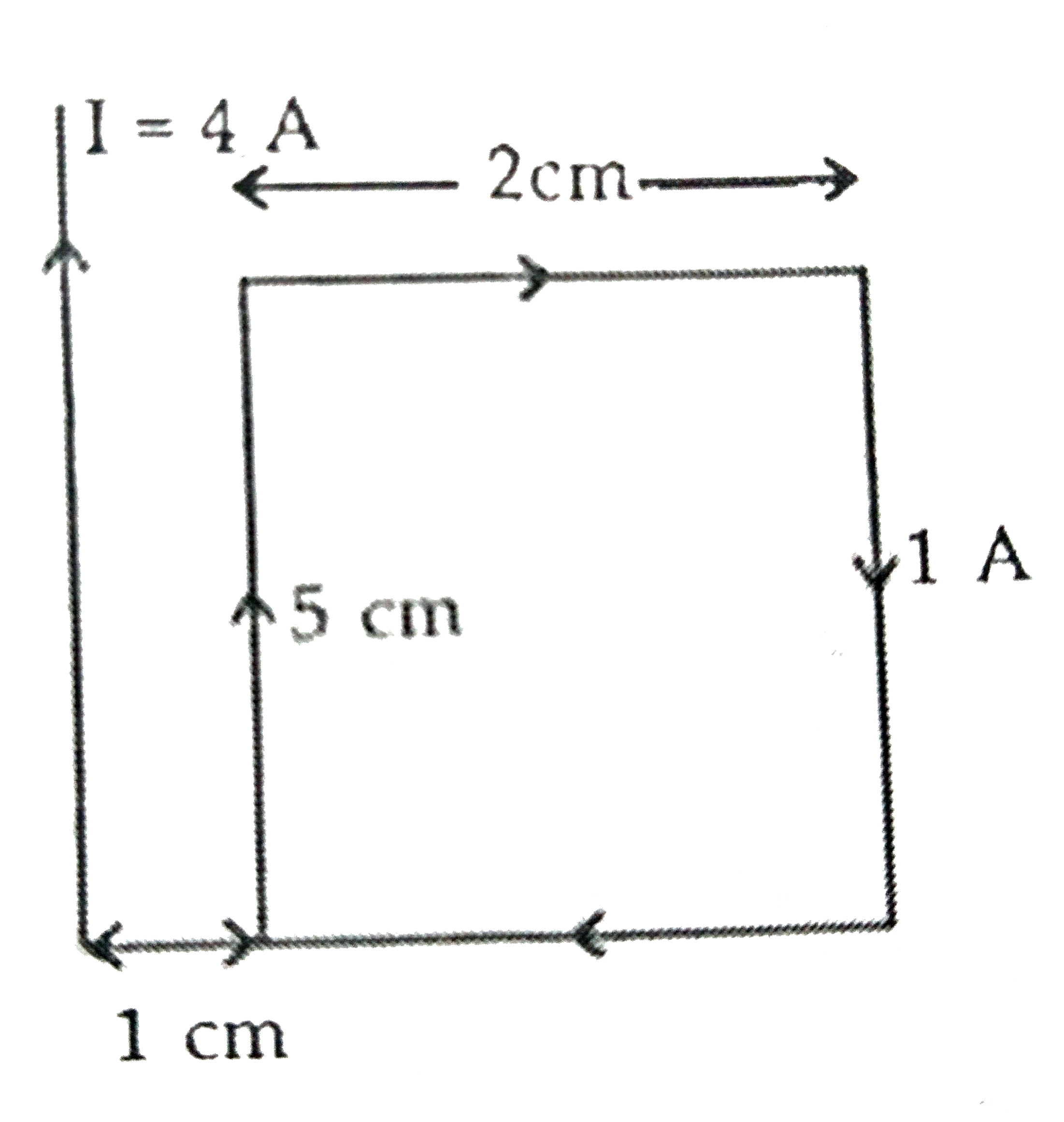
View SolutionA rectangular loop of wire of size 2 cm xx 5cm carries a steady current of 1A. A straight long wire carrying 4 A current is kept near the loop as shown. If the loop and the wire are coplanar, find (i) the torque acting on the end (ii) the magnitude and direction of the force on the loop due to the current carrying wire.
View Solution(a) Dfine mutaul indutace and write its S.I. unit.
(b) A square loop of side 'a' carrying a current is kept at distance x from an infinitely long straight wire carrying a current as shown in thefigure. Obtain the expression for the resultant force on the loop.

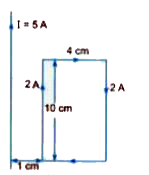
View SolutionA rectangular loop of wire of size 4 cm xx 10 cm carries a steady current of 2A. A straight long wire carrying 5A current is kept near the loop If the loop and the wire are coplanar, find (i) the torque acting on the loop and (ii) the magnitude and direction of the force on the loop due to the current carrying wire(fig).
View SolutionA rectangular loop of wire of size 4 cm 10 cm carries a steady current of 2A. A straight long wire carrying 5A current is kept near the loop (fig). If the loop and the wire are coplanar, find
(i) the torque acting on the loop and
(ii) the magnitude and direction of the force on the loop due to the current carrying wire.
View SolutionA square loop of side 15 cm carrying current of 10 A is kept at a distance of 5 cm from a long wire carrying 12 A current as shown in the adjoining figure. Calculate the net force acting on the loop.
View SolutionA current carrying squre loop is placed near an infinitely long current carrying wire as shown in figure . The loop torque acting on the loop is
View SolutionA rectangular loop carrying a current , is situated near a long striaght wire carrying a steady current . The wire is parallel to one of the sides of the loop and is in the plane of the loop as shown in the figure. Then the current loop will
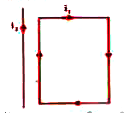
View SolutionA rectangular loop carrying a current is situated near a long straight wire such that the wire is parallel to one of the sides of the loop and is in the plane of the loop . If steady current is established in the wire as shown in the figure ,
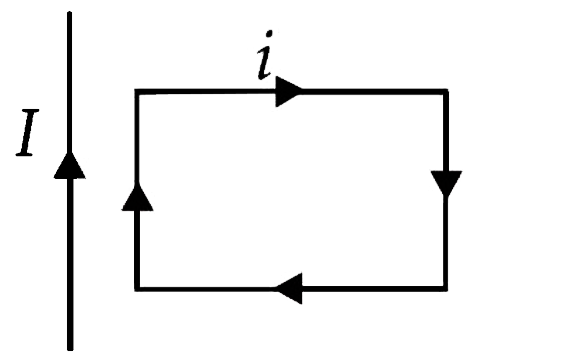
View SolutionA rectangular loop carrying a current i is situated near a long straight wire such that the wire is parallel to one of the sides of the loop and is in the plane of the loop . If steady current I is established in the wire as shown in the figure ,
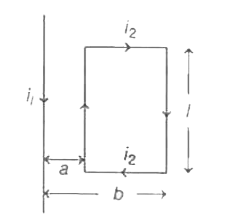
View SolutionIn the figure, a long straight wire carrying a current and a loop of a square conducting wire of side l are located at a distance 'a' from the current carrying wire, both the current carrying wire and the loop are in the plane of the paper, find the magnetic flux of the current carrying wire passing through the loop Do it
View SolutionA current carrying square loop is placed near a straight infinitely long current carrying wire as shown in the figure. The torque acting on the loop is
View Solution