Using Bohr’s postulates obtain the expression for i kinetic energy and ii potential energy of the electron in stationary state of hydrogen atom. Draw the energy level diagram showing how the transitions between energy levels result in the appearance of Lymann Series.
If electron moves on a circular path of radius r with speed v as shown in fig.So the KE of the electron
Related Solutions
Using Bohr's postulates, obtain the expressions for (i) kinetic energy and (ii) potential energy of the electron in stationary state of hydrogen atom.
Draw the energy level diagram showing how the transitions between energy levels result in the appearance of Lymann Series.
View SolutionUsing Bohr's postulates, obtain the expression for the total energy of the electron in the stationary states of the hydrogen atom. Hence draw the energy level diagram showing how the line spectra corresponding to Balmer series occur due to transition between energy levels.
View SolutionUsing Bohr's postulates, obtain the expression for the total energy of the electron in the stationary states of the hydrogen atom. Hence draw the energy level diagram showing how the line spectra corresponding to Balmer series occur due to transiton between energy levels.
View SolutionObtain an expression for energy of orbital electron in hydrogen atom using Bohr’s postulates.
View SolutionExplain the meaning of the terms: Energy level, excitation potential, ground state. Write down the names of the series obtained in hydrogen spectrum. Drawing the excited energy diagram of hydrogen atom, show these series on an energy level diagram.
View SolutionUsing Bohr's postulates , obtain the expreesion for the total energy in the stationary states of hydrogen atom . Hence , draw the energy level diagram showing how the line spectra corresponding to Balmer series occur due to transition between energy levels.
View SolutionDraw energy level diagram for hydrogen atom and show the various line spectra originating due to transition between energy levels.
View SolutionDraw the energy level diagram showing how the spectrallines corresponding to Balmer series occur due to transition between the energy levels.
View SolutionWhat is the energy level diagram for an atom? Calculate the energies of the various energy levels of a hydrogen atom and draw an energy level diagram.
View SolutionDraw energy level diagram for Hydrogen atom showing at least four lowest energy levels. Show the transitions responsible for emission of Balmer series.
View SolutionDraw the energy level diagram to show different series of hydrogen atoms.
View SolutionDraw energy level diagram for Balmer series for transition between eriergy levels.
View SolutionDraw the energy level diagram of hydrogen atom and show the transitions responsible for :
(i) absorption lines of Lyman series.
(ii) emission lines of Balmer series.
View SolutionThe diagram shows the energy level for an electron in a hydrogen atom. Which transition, shown here, represents the emissions of a photon of maximum energy?
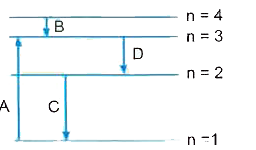
View Solutionहाइड्रोजन परमाणु की मूल ऊर्जा स्तर की ऊर्जा - हैं इस अवस्था में इलेक्ट्रॉन की गतिज ऊर्जा एंव स्थितिज ऊर्जा की गणना कीजिए ।
View SolutionDraw the energy level diagram of hydrogen atom. Calculate the energy value upto fifth excited energy states of hydrogen.
View SolutionState Bohr’s postulates for atomic model and using them derive an expression forthe total energy of an electron revolving in a stationary nth orbit of hydrogen atom.
View Solutionपरमाणु का ऊर्जा स्तर क्या हैं ? हाइड्रोजन परमाणु के विभिन्न ऊर्जा स्तर की ऊर्जा की गणना कीजिए तथा इसका आरेख बनाइए ।
View SolutionDraw a neat labelled energy level diagram for H-atom showing the transitions.
View SolutionDraw a neat, labelled energy level diagram for H atom showing the transitions.
Explain the series of spectral lines for H atom. Whose fixed inner orbit numbers are 3 and 4 respectively.
The work function for potassium and caesiumare 2.25 eV and 2.14 eV respectively. Is the photoelectric effect possible for either of them if incident wavelength is 5180 Å ?
[Given : Planck's constant , Velocity of light ]
View Solution