If E1 ≡ a1x + b1y + c1z + d1 = 0 and E2 ≡ a2x + b2y + c2z + d2 = 0 be the two intersecting planes where L is their line of intersection then determine the symmetric form of the line L.
Let vector n1 = a1 b1 c1 and vector n2 = a2 b2 c2 which are the normals of E1 = 0 and E2 = 0 respectively. Hence the line L is parallel to vector n1 x n2 so that the DRs of the line L are b1c2 - b2c1 c1a2 - c2a1 a1b2 - a2b1. Now we find a point on L. Since one of the DRs is not zero we consider that a1b2 - a2b1 ≠ 0. Therefore the equations a1x + b1y = - d and a2x + b2y = - d2 have unique solutionsso that the point x y 0 lies on L. Therefore the symmetric form of L is
Related Solutions
Determine the symmetric form of the equation to the line of intersection of the plane and .
View SolutionThe lines l and m intersect at point A. The point P is equidistant from these lines. Show that the line AP intersects the angle formed between l and m.
View Solutionमाना कि L, समतलों और की प्रतिच्छेदन रेखा से गुजरने वाली रेखा हैं। तब, (2, 1, 4) से होकर गुजरने वाले और रेखा L के लंबवत समतल का समीकरण है:
View SolutionIn the figure below, l and m are two intersecting lines and P || l and q || m. Prove that p and q are also intersecting lines.
View SolutionIf lines l and m intersect at a point Also m and n intersect at a point, is it necessary that lines l,m,n intersect at the same point.
View SolutionAP and BQ are bisectors of two parallel intersections that are formed from the intersection of the parallel lines l and m by the oblique line t (figure). Show that AP || BQ is.
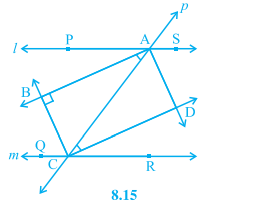
View Solutionਦੋ ਸਮਾਂਤਰ ਰੇਖਾਵਾਂ l ਅਤੇ m ਨੂੰ ਇਕ ਕਟਾਵੀਂ ਰੇਖਾ p ਕਟਦੀ ਹੈ (ਦੇਖੋ ਚਿੰਤਰ 8.15)। ਦਰਸਾਉ ਕਿ ਅਦਰਲੇ ਕੋਣਾਂ ਦੇ ਸਮਦੁਭਾਜਕਾਂ ਨਾਲ ਬਣੀ ਚਤੁਰਭੁਜ ਇਕ ਆਇਤ ਹੈ।
View SolutionLet L be the line through the intersection of the planes and . Then, the equation of the plane passing through and perpendiculr to the line L is
View SolutionEquations of the line of intersection of the two planes y = b , z = c in the symmetrical form are
View SolutionThe equation of any circle passing through the points of intersection of the circle S=0 and the line L=0 is
View SolutionLine L Delta OAB Does not intersect the arm of
View SolutionThe line intersect the coodinate axes at A and B respectively. A line L bisects the area and perimeter of triangle OAB where 'O' is origin
The number of possible such lines is
View SolutionShow that the locus of a point, equidistant from two intersecting lines in the plane, is a pair of lines bisecting the angles formed by the given lines.
View SolutionLet L be the line joing the origin to the point of interesection of the lines represecnted by . If L is perpendicular to the line kx+y+3=0, then k=
View SolutionLet L be the line joing the origin to the point of interesection of the lines represecnted by . If L is perpendicular to the line kx+y+3=0, then k=
View SolutionLet L be the line joining the origin to the point of intersection of the lines represented by . If L is perpendicular to the line then
View SolutionFor a point P in the plane, let d1 (P) and d2 (P) be the distance of the point P from the lines x – y = 0 and x + y = 0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2 < d1(P) + d2 (P)< 4, is
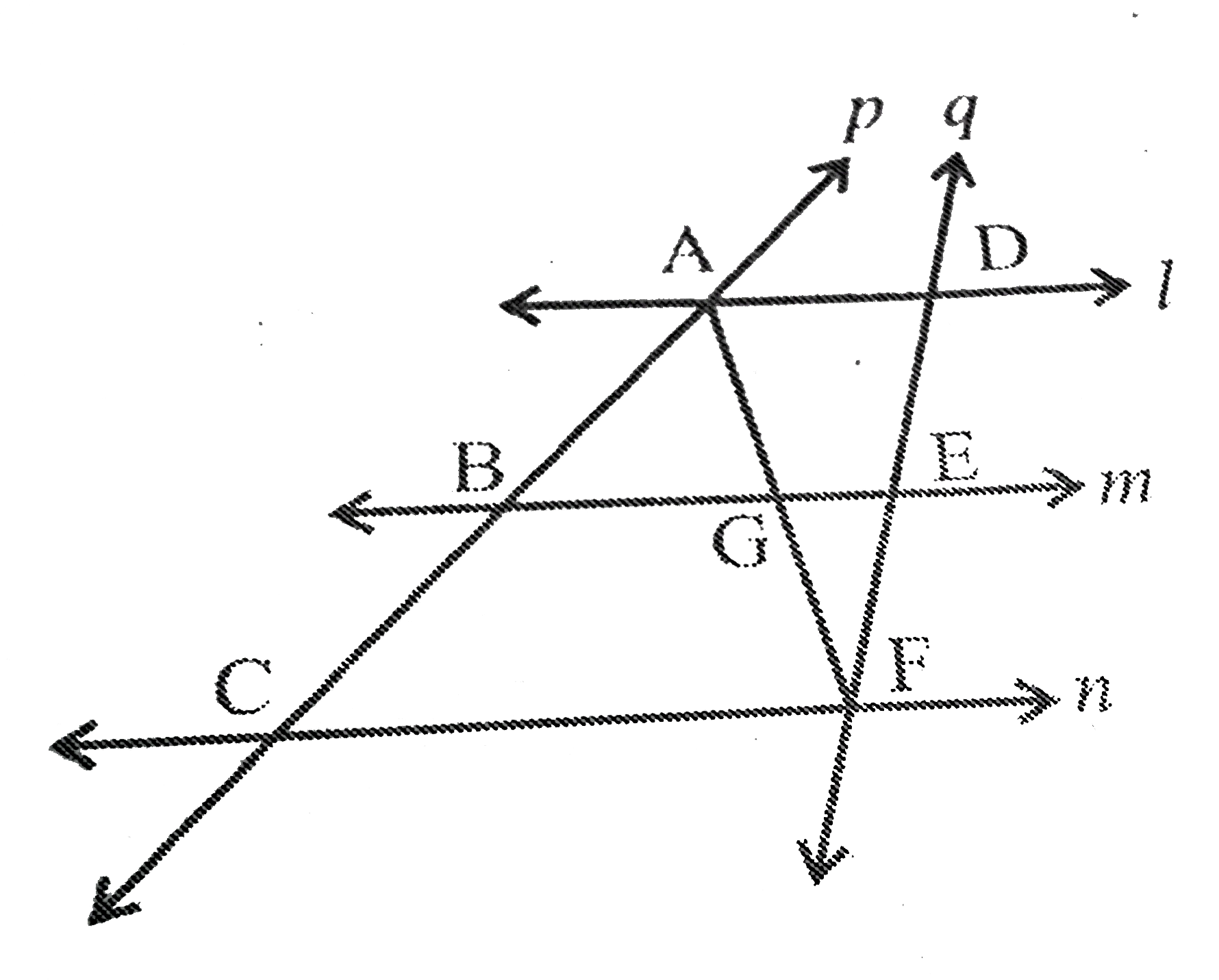
View Solutionl , m और n तीन समांतार रेखाएँ है , जो तिर्यक रेखाओं p और q द्वारा इस प्रकार प्रतिच्छेदित हैं कि और n रेखा p पर सामान अंत : खंड AB और BC काटती हैं ( देखिए आक्रति 8.28 ) | दर्शाइए कि और रेखा q पर भी सामान अंत : खंड DE और EF कटती हैं ।
View SolutionThe point C is the image of point A in line l and line segment BC intersects the line l at P.
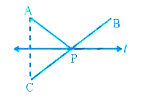
Is PA = PC ?
View SolutionThe point C is the image of point A in line l and line segment BC intersects the line l at P.
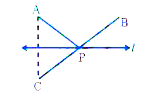
Is the image of P in line l the point P itself ?
View Solution