The difference of the focal distances of any point on the hyperbola is constant.
Let Px y be any point on the hyperbola whose centre is the origin C foci are S S directries are ZM and ZM as shown in fig. Let PN PM PM be the perpendiculars drawn from P upon x–axis and the two directrices respectively. Now SP = ePM = eNZ = eCN – CZ. ∴ SP = ex - a/e = ex - a.and SP = ePM = eNZ = eCN + CZ= ex + a/e = ex + a∴ SP – SP = 2a. By the above theorem the hyperbola is sometimes defined as the locus of a point the difference of whose distances from two fixed points is constant.
Related Solutions
The sum of the focal distances of a point on the ellipse is
View SolutionThe difference of the focal distance of any point on the hyperbola is equal to its
View SolutionThe difference of the focal distance of any point on the hyperbola is equal to its
View SolutionThe difference of the focal distance of any point on the hyperbola is equal to its
View SolutionMatch the numerical difference of the focal distance of any point on the hyperbolas
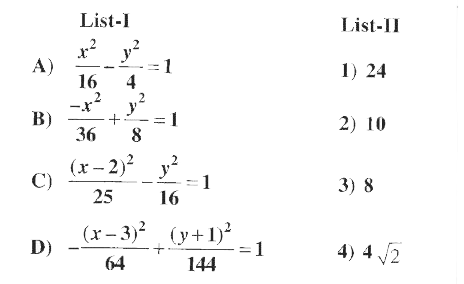
The correct Match is
View SolutionThe difference of the focal distances of any point on the hyperbola is equal to its
View SolutionShow that the difference of focal distances of any point of the hyperbola is constant.
View Solutionकिसी अतिपरवलय पर स्थित किसी बिंदु की नाभीय दूरियों का अंतर किसके बराबर है?
View SolutionIf the length of the transverse and conjuigate axes of hyperbola be 8 and 6 respectively, then the difference of focal distance of any point of the hyperbola will be
View SolutionIf the length of the transverse and conjugate axes of a hyperbola be 8 and 6 respectively, then the difference focal distances of any point of the hyperbola will be
View SolutionIf the length of the transverse and conjuigate axes of hyperbola be 8 and 6 respectively, then the difference of focal distance of any point of the hyperbola will be
View Solutionयदि किसी अतिपरवलय के अनुप्रस्थ तथा संयुग्मी अक्ष क्रमशः 8 तहत 6 हो , तो अतिपरवलय के किसी बिन्दु की नाभीय दूरियों का अंतर होगा।
View SolutionThe difference of the focal distance of any point on the hyperbola is
View SolutionThe difference of the focal distance of any point on the hyperbola 9x ^(2) -16 y ^(2) =144, is
View SolutionThe difference of focal distance of any point on the hyperbola is
View SolutionShow that the difference of the focal distances of any point on the hyperbola is equal to its transverse axis.
View SolutionShow that the difference of the focal distances of any point on the hyperbola is equal to its transverse axis.
View SolutionThe difference of focal distances of any point on a hyperboal is equal to-
View Solutionshow that the absolute value of the focal distances of any point P on the hyperbola in the length of its transverse axis.
View SolutionIn a rectangular hyperbola, prove that the product of the focal distances of a point on it is equal to the square of its distance from the centre of the hyperbola .
View Solution