Find the equation of the tangent at the point 30° parametric value of θ of the circle is x2 + y2 + 4x + 6y – 39 = 0.
Equation of the circle is x2 + y2 + 4x + 6y – 39 = 0g = 2 f = 3 r = √4 + 9 + 39 = √52 = 2√3 θ = 30° Equation of the tangent is
Related Solutions
Find the equation of the tangent at the
point (parametric value of ) of the
circle is .
View SolutionFind the equation of the tangent at the
point (parametric value of ) of the
circle is .
View SolutionFind the polar of the point (−2,3) with respect to the circle x2+y2−4x−6y+5=0
View Solution2.10 The radii of the circles x2 + y2 = 1, x2 + y2 – 2x – 6y = 6 and x2 + y2 - 4x - 12y = 9 are in(A)AP.(B)GP.(C) H.P.(D) None
View SolutionFind the equation of the radical axis of the following circles. is
View SolutionFind the equations of the tangents from the point A(3,2) to the circle .
View SolutionFind the equations of the tangents from the point A(3,2) to the circle .
View SolutionFind the parametric equation of the circles :
View SolutionFind the parametric equation of the circles :
View SolutionFind the parametric equation of the circles :
.
View SolutionFind the parametric equations of the circles
View SolutionConsider a circle x2 + y2 =4 and a point P(4,2). O denotes the angle enclosed by the tangents from Ponthe circle and A, B are the points of contact of the tangents from Pon the circle.2.5The value of lies in the interval(A) (0,15^@) (B) (15^@, 30^@)(C) 30^@, 459)(D) (45^@, 60^@)The internant mo
View Solution. Find current enclosed in the loopMagnetic field at a point (x, y, z) is given by B- Boyix2 + y = 2(x2 + y2)2__Box(x2 + y2)2
View SolutionObtain the parametric equation of each
of the following circles.
View SolutionFind the equation of the tangent to the circle x^2+y^2-4x-6y-12=0 at (-1,-1)
View SolutionFind the length of a tangent drawn from the point to the circle
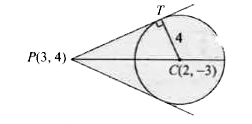
View SolutionFind the parametric representation of the circle 3x^2+3y^2-4x+6y-4=0
View SolutionEquation of a chord with a middle point | Parametric form of circle | Equation of common tangents | Parametric form of circle based Questions
View SolutionThe parametric equation of the circle are
View SolutionThe parametric equation of the circle are
View Solution