Derive the expression for normal and shear stress on a plane AE inclined at an angle B with AB subjected to direct stresses of compressive nature both of σx and σy on two mutually perpendicular stresses as shown in fig.
Consider the unit thickness of the element. Applying equations of equilibrium to the free body diagram of wedge ABE. Let σn and τ be the normal and shear stresses on the plane AE.∑Fx = 0 σx BE – τ AE cos θ − σn AE cos 90 – θ = 0 σx BE + τ AE cos θ + σn AE sin θ = 0 ...i ∑Fy = 0 σy AB + τ AE sin θ − σn AE sin 90 – θ = 0 σy AB + τ AE sin θ − σn AE cos θ = 0 ...ii Dividing equations i and ii by AE and replacingsin θ = BE/ AE and cos θ = AB/ AE – σx sin θ + τ cos θ + σn sin θ = 0 ...iii – σx cos θ + τ sin θ – σn cos θ = 0 ...iv Multiplying equation iii by sin θ iv by cos θ and subtracting – σx sin2 θ + σn sin2 θ – σy cos2 θ + σn cos2 θ = 0 σn = σx sin2 θ + σy cos2 θ Putting cos2 θ = 1 + cos 2θ/ 2and sin2 θ = 1 - cos 2θ/2 Also multiplying iii by cos θ and 4 by sin θ and then adding. − σx sin θ cos θ + τ cos2 θ + σy cos θ sin θ + τ sin2 θ = 0 τ = σx + σy sin θ cos θ or τ = σx + σy/2sin 2θ
Related Solutions
Shearing Stress And Tangential Stress
View SolutionConsider a long steel bar under a tensile stress due to force F acting at the edges along the length of the bar (as shown in figure). Consider a plane making an angle with the length. What are the tensile and shearing stresses on this plane? (a) For what angle is the tensile stress a maximum ? (b) For what angle is the shearing stress a maximum ?
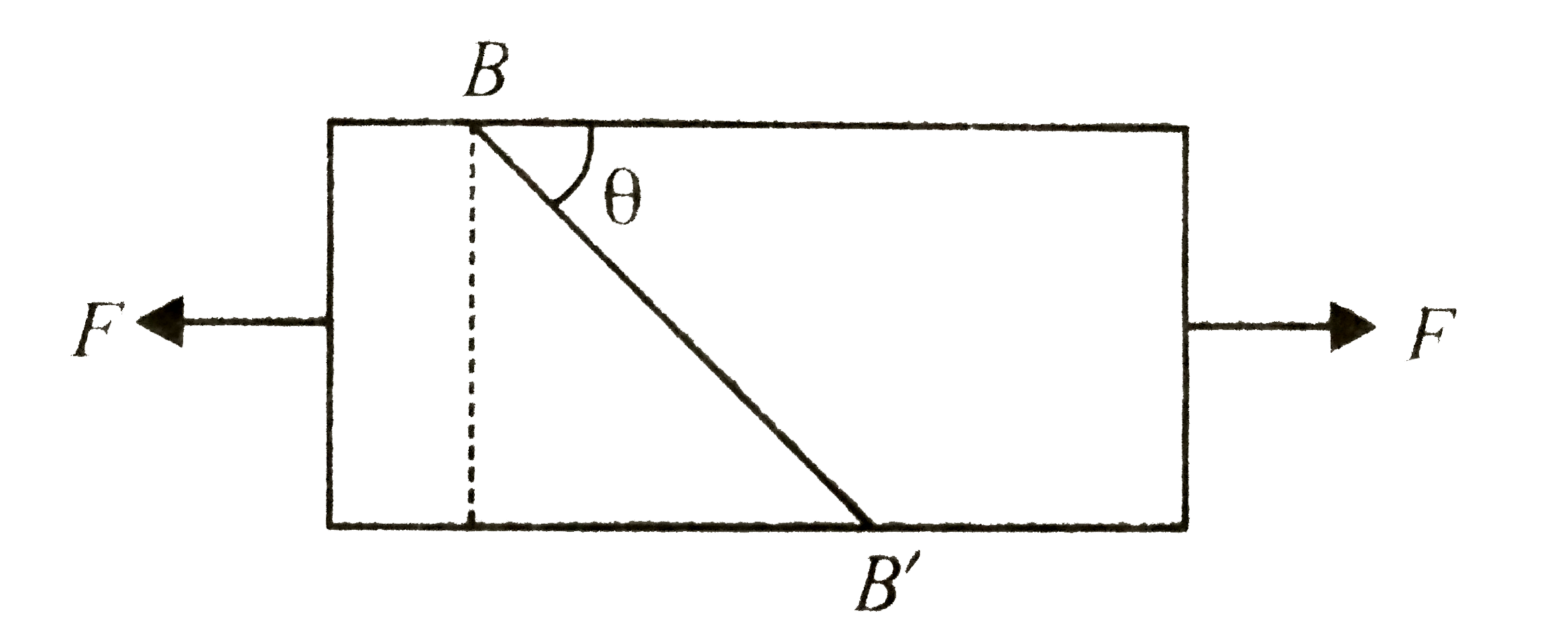
View SolutionA bar of cross- sectional area A is is subjected two equal and opposite tensile forces at its ends as shown in figure. Consider a plane BB' making an angle with length. The ratio of tensile stress to the shearing stress on the plane BB' is
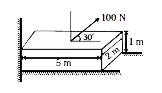
View Solutionचित्र में दिखाए गए स्थिर ब्लॉक के लिये अनुदैर्ध्य प्रतिबल तथा अपरूपण प्रतिबल ज्ञात करो।
View SolutionHow many times the shearing stress of fluid is to the shearing stress of solid ?
View SolutionShear stress.
View SolutionElasticity: Longitudinal Stress & strain | Shear stress & shear strain | Volumetric stress and strain
View SolutionDefine Tensile stress or compressive stress?
View SolutionExplain tensile stress and compressive stress.
View SolutionThe ratio of shear stress to shear strain is ...
View SolutionConsider a long steel bar under a tensile stress due to forces F, acting at the edges along the length of the bar Consider a plane making an angle theta with the length. What are the tensile and shering stresses on this plane ? (a) For what angle is the tensile stress a maximum ? (b) For what angle is the shearing stress a maximum ?
View SolutionConsider a long steel bar under a tensile stress due to forces F, acting at the edges along the length of the bar Consider a plane making an angle theta with the length. What are the tensile and shering stresses on this plane ? (a) For what angle is the tensile stress a maximum ? (b) For what angle is the shearing stress a maximum ?
View SolutionIn the above problem, for what angle is the shearing stress a maximum?
View SolutionWhat is shearing (tangential) stress?
View SolutionShear stress plays is related to
View SolutionThe shearing stress is that in which there is a change in _____.
View SolutionShear stress plays is related to
View SolutionExplain what is Shearing stress?
View Solutionअपरूपण प्रतिबल क्या है ?
View SolutionShearing stress causes change in
View Solution