In Column I a family of concurrent lines is given and their points of concurrence are given in Column II. Match the items of Column I with those of Column I with those of Column II.A If a b c are real as 2a + 3b + c = 0 then the lines ax + by + c = 0 are concurrentP 2/5 3/5B If a is a parameter then the family of lines 1 + ax + 2 - a y + 5 = 0 is concurrent atq 2 3C The lines a dx + ay + a + d = 0 for different values of d are concurrent atr 1 2D For different values m and n the lines m + 2nx + m - 3ny m + n = 0 are concurrent ats -5/3 -5/3t 1 -2
A 2a + 3b + c = 0 ⇒ ax + by + c = 0 passes through 2 3.Answer: A → qB The equation 1 + ax + 2 - ay + 5 = 0 is written as x + 2y + 5 + ax - y = 0 Hence the line passes through the intersection of the lines x + 2y + 5 = 0 and x - y = 0 and the point of intersection is -5/3 -5/3Answer: B → sC The equation a - dx + ay + a + d = 0 is written as ax + y + 1 + d 1 - x = 0 so that this line passes through the intersection of the lines 1 - x = 0 and x + y + 1 = 0 which is given by 1 -2.Answer: C → tD The equation m + 2nx + m - 3ny - m + n = 0 is written as mx + y -1 = 0 . Hence the line passes through the intersection of the lines x + y - 1 = 0 and 2x - 3y + 1 = 0 which is given by 2/5 3/5.Answer: C → p
Related Solutions
Match item in column I with those given in column II. Column 1
View SolutionMatch items given in Column I with those given in Column II

View SolutionMatch the items of Column-I with those in Column-II

View SolutionMatch the items of Column-I with those in Column-II

View SolutionMatch the items of Column-I with those in Column-II
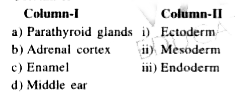
View SolutionMatch items in Column I with those in Column II:
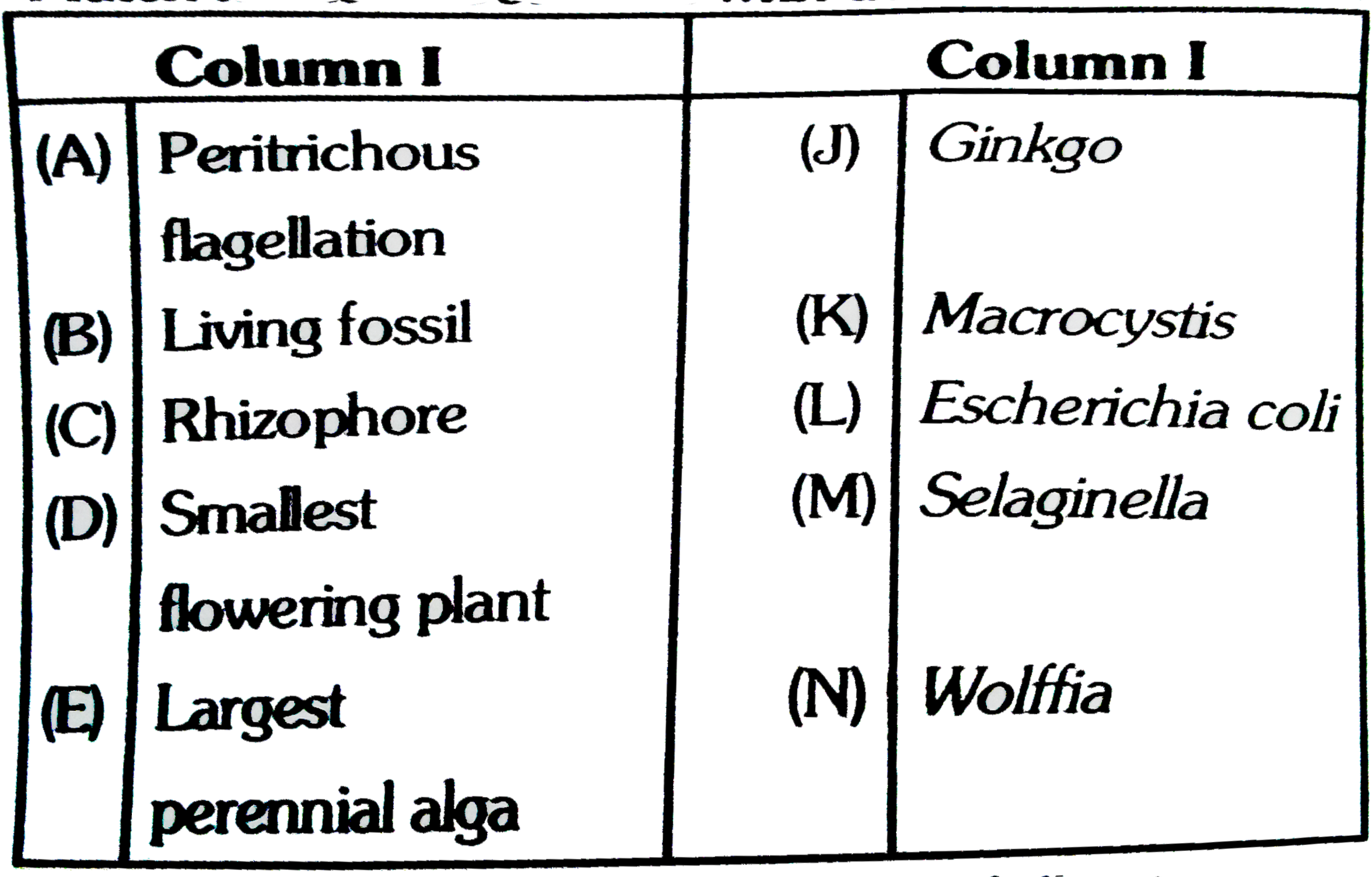
View SolutionMatch items in Column I with those in Column II

View SolutionMatch items in Column I with those in Column II.
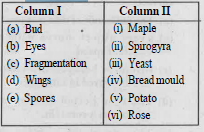
View SolutionMatch items in Column I with those in Column II:
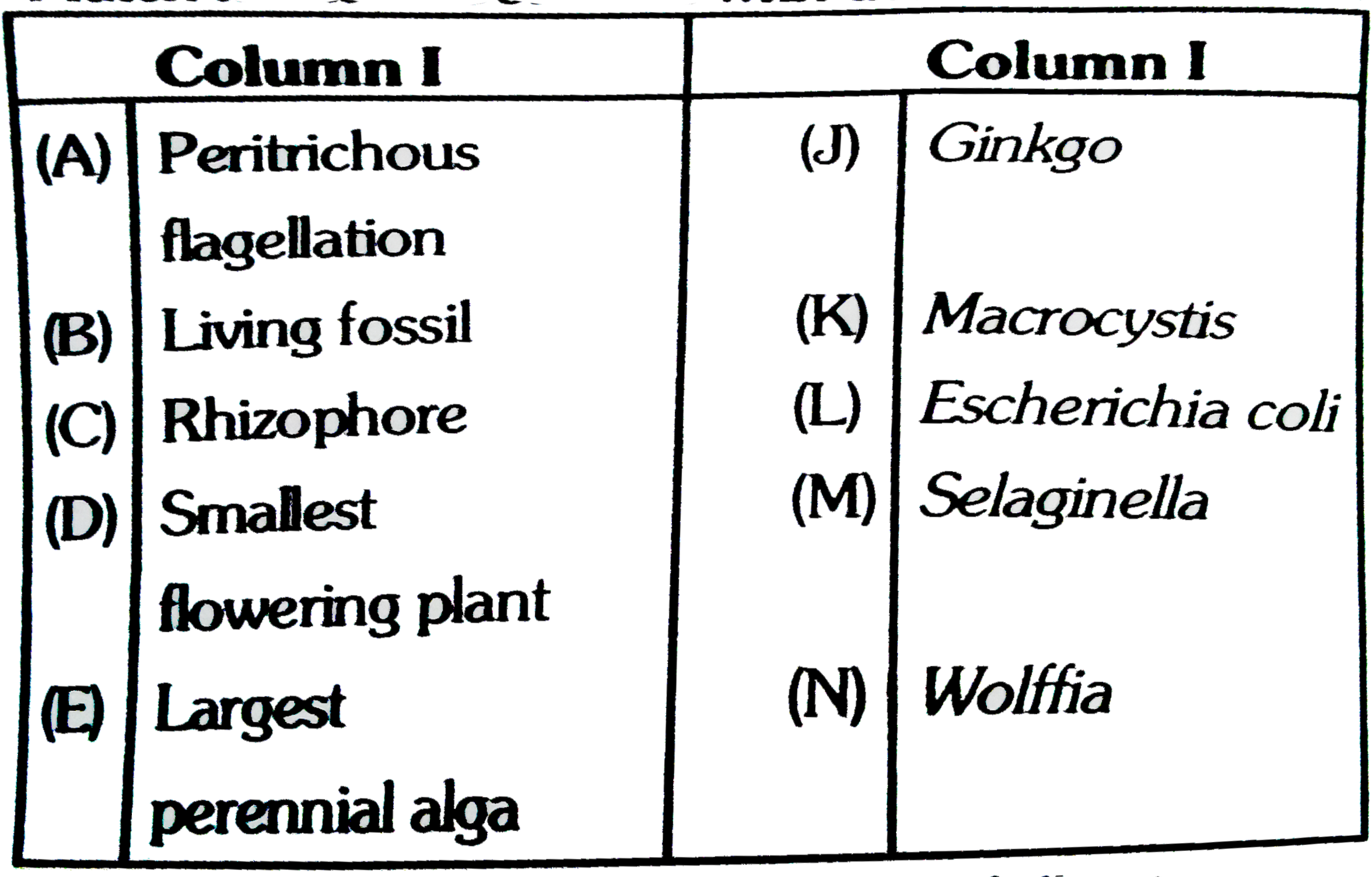
View SolutionMatch items in Column I with those in Column II.
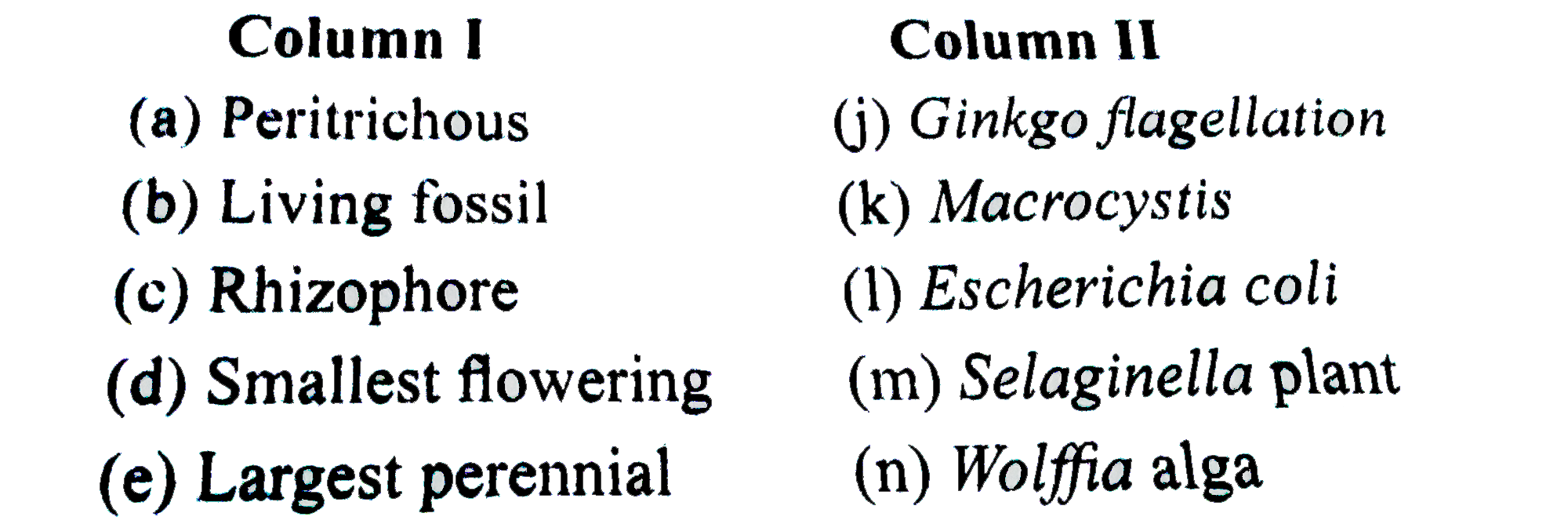
View SolutionMatch the items in column I with those in column II
View SolutionMatch the items in Column I with those in Column II
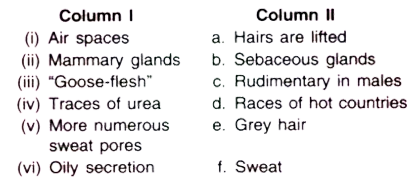
View SolutionMatch the items in column I with those in column II :
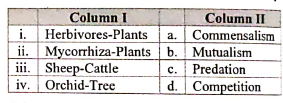
View SolutionMatch the items in Column I with those in column II:
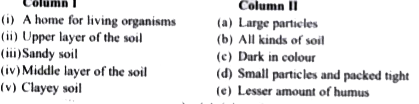
View SolutionMatch the items in Column I with those in Column II :
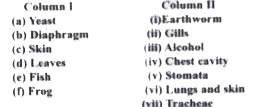
View SolutionMatch the items in column I with those in column II :
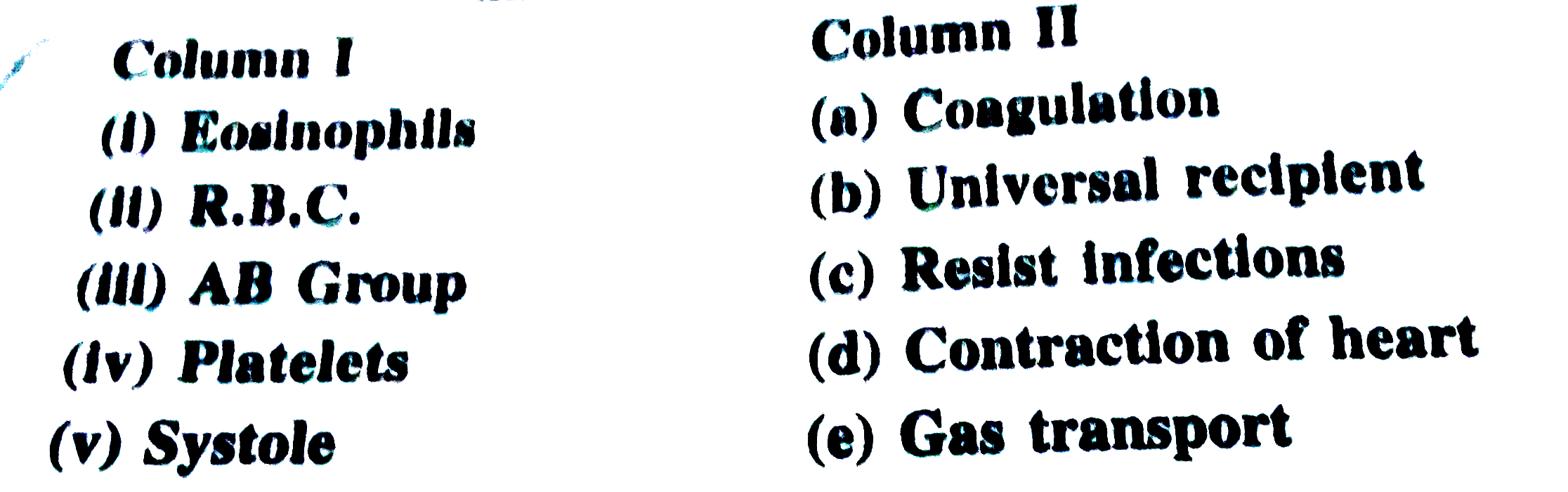
View SolutionMatch the items of Column-I with those of Column-II:

View SolutionMatch the items of Column I with those of Column II.
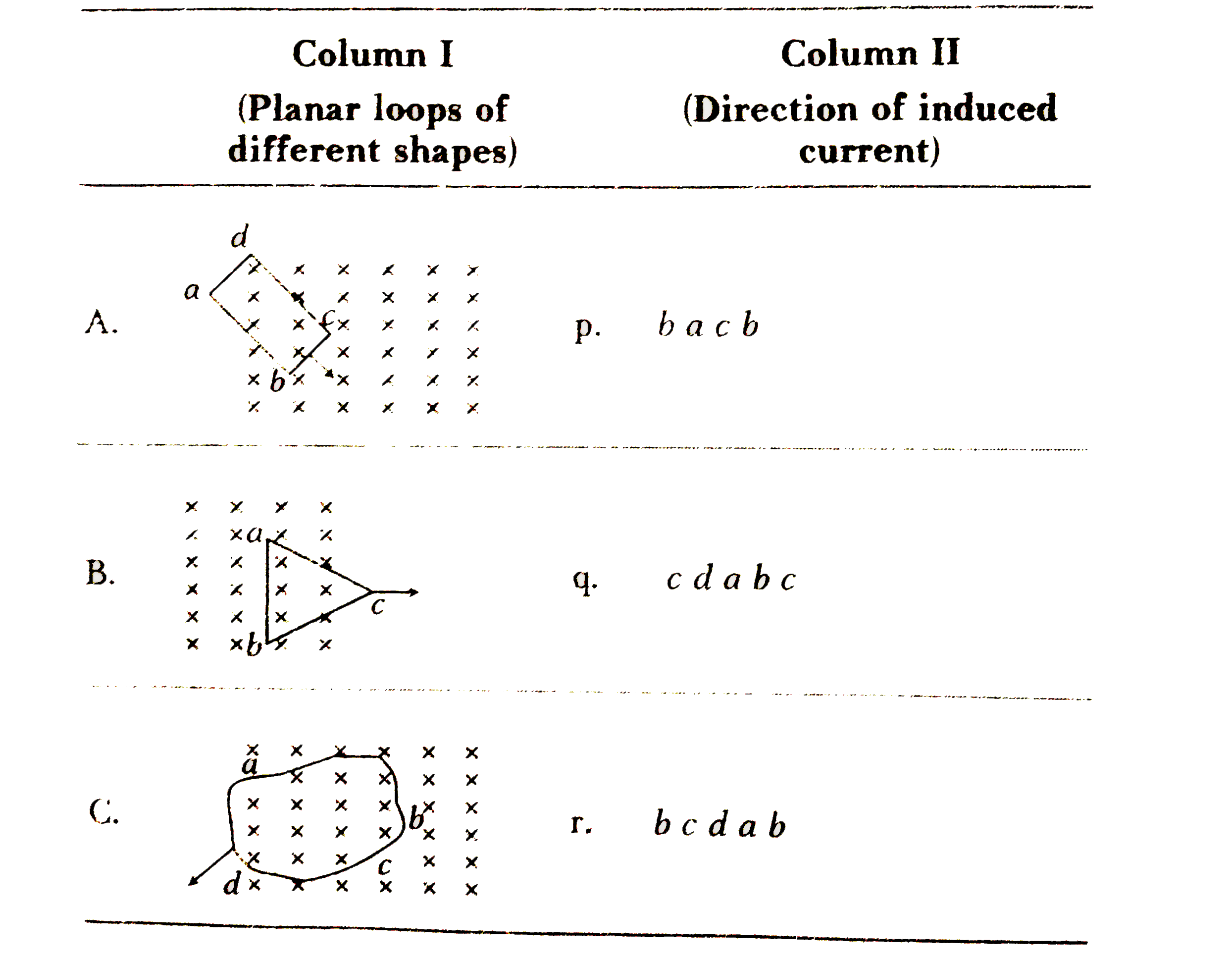
View SolutionMatch the items of Column I with those of Column II.
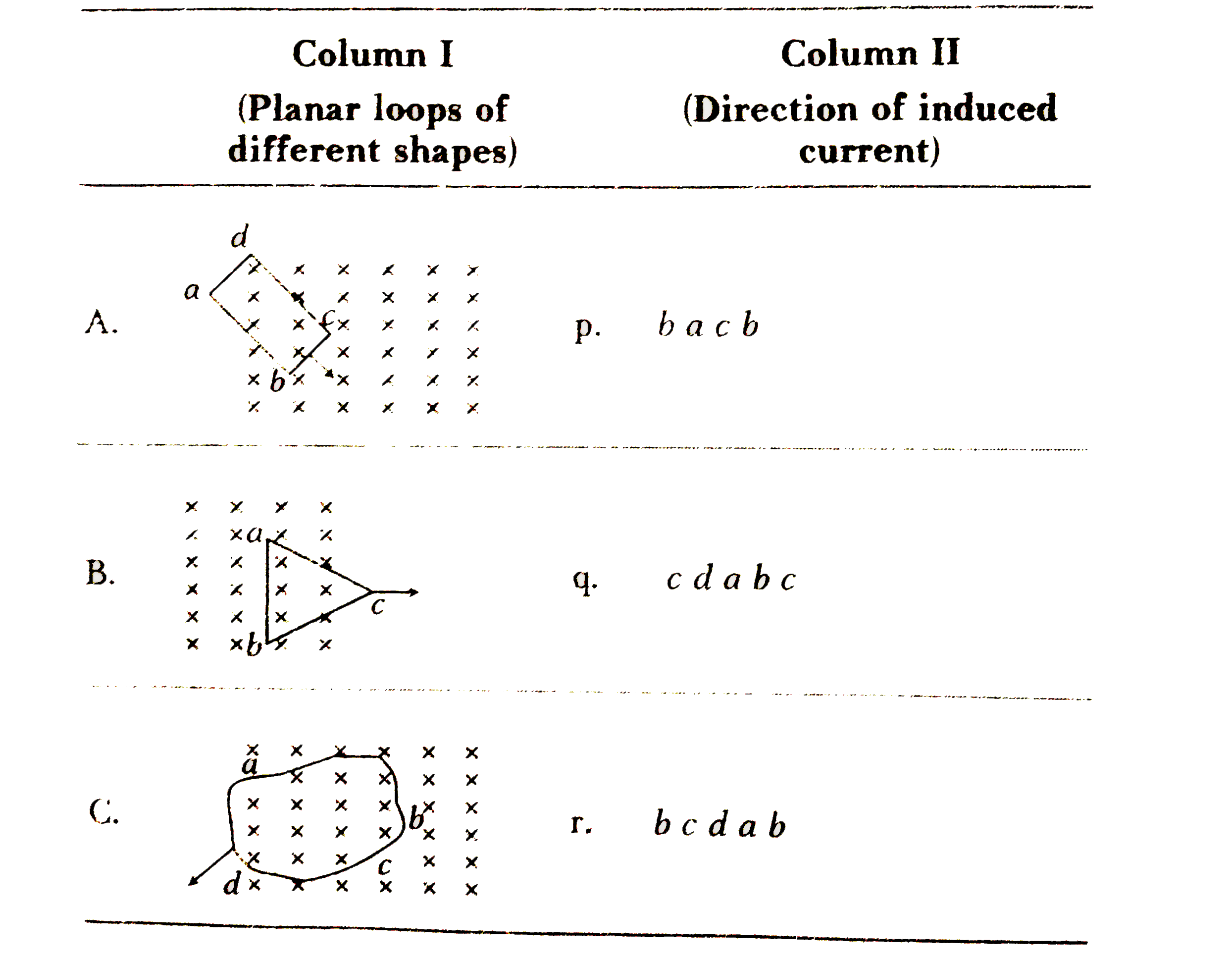
View SolutionMatch the items of column I with those of column II:
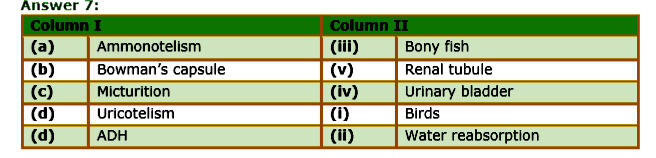
View Solution