For the circuit in Fig. given that L = 0.159 H C = 0.3183 mf I2 = 5 ∠ 60° A V1 = 250 ∠ 90° volts. Find :- i Impedance Z1 with its components. ii Source voltage in the form of Vm cos ωt + φ. iii Impedance Z2 with its components so that source p.f. is unity without adding to the circuit power loss. iv Power loss in the circuit v Draw the phasor diagram.
XL = 314 × 0.159 = 50 ohms XC = 1/314 × 0.3183 × 10−3 = 10 ohms IL = V1/jXL = 250 ∠90º/50 ∠ 90º = 5 ∠ 0º amps V2 = −jI2 XC = 5 ∠ 60º × 10 − ∠ 90º = 50 − ∠ 30º volts = 43.3 −j 25 volts IL = IL −I2 = 5 ∠ 0º − 5 ∠ 60º = 5 + j0 − 5 0.5 + j0.866 = 2.5 −j4.33 = 5 ∠− 60º a Z1 = V2/I1 = 50 ∠ − 30º/5 ∠− 60º = 10 ∠ + 30º = 10 cos 30º + j sin 30º = 8.66 + j5 b Vs = V1 + V2 = 0 j250 + 43.3 −j25 = 43.3 + j225 = 229.1 ∠ 79.1º volts Vs has a peak value of 229.1 × 2 = 324 volts Vs = 324 cos 314 t − 10.9º taking V1 as reference or Vs = 325 cos 314 t − 79 .1º taking IL as reference. c Source Current must be at unity P.f. with Vs Component of IL in phase with Vs = 5 cos 79.1º = 0.9455 amp Component of IL in quadrature with VS and is lagging by 90º = 5.00 × sin 79.1º = 4.91 amp Z2 must carry Ia such that no power loss is there and IS is at unity P.f. with Vs . Ia has to be capacitive to compensate in magnitude the quadrature component of IL |Ia| = 4.91 amp |Z2|= Vs/| Ia| = 229.1/4.91 = 46.66 ohms Corresponding capacitance C2 = 1/46.66 × 314 = 68.34 μF d Power-loss in the circuit = I21 × 8.66 = 216.5 watts or power = Vs × component of IL in phase with Vs = 299.1 × 0.9455 = 216.5 watts e Phasor diagram is drawn in Fig.Phasor diagram
Related Solutions
Find in an alternating LR circuit, (i) resultant voltage (ii) impedance of circuit, (iii) Phase difference, (iv) average power.
View Solutionप्रत्यावर्ती L -C परिपथ में निम्नलिखित ज्ञात कीजिए- (i) परिणामी वोल्टेज (ii) परिपथ की प्रतिबाधा (iii) अनुनाद धारा की आवृत्ति (iv) औसत शक्ति क्षय
View Solutionएक L-C-R श्रेणी परिपथ में तथा एक प्रत्यावर्ती स्त्रोत से जुड़े है | ज्ञात किजिये-
(i) स्त्रोत की आवृत्ति, (ii) प्रतिघात, (iii) प्रतिबाधा, (iv) परिपथ में धारा, (v) विभिन्न अवयवों के सिरों का विभवांतर, (vi) धारा तथा वोलटता के बीच कलांतर (vii) शक्ति गुणांक (viii) परिपथ में औसत विघुत शक्ति क्षय (ix) अनुनादी आवृत्ति, (x) अनुनाद की स्थिति में परिपथ में प्रतिबाधा तथा धारा |
View SolutionIf the power factor in a circuit is unity, then the impedance of the circuit is
View Solutionप्रत्यावर्ती L-C-R परिपथ में ज्ञात कीजिए-
(i) परिणामी वोल्टेज, (ii) परिपथ की प्रतिबाधा, (iii) परिणामी वोल्टेज और धारा के मध्य कलान्तर, (iv) औसत शक्ति व्यय|
View Solutionदिये गये चित्र में एक LCR परिपथ दिखाया गया है एक प्रत्यावर्ती धारा स्त्रोत वोल्टता परिपथ से जुड़ा है परिपथ के लिए गणना कीजिए -(i ) प्रतिबाधा (ii ) शक्ति गुणांक ।(iii ) धारा का शिखर मान ।
View Solutionसंग्लन चित्र में एक परिपथ दिखाया गया है|प्रत्यावर्ती धारा-स्त्रोत की वोल्टता से प्रदर्शित है|परिपथ के लिए गणना कीजिए:(i ) प्रतिबाधा,(ii ) शक्ति-गुणांक तथा (iii ) धारा का शिखर मान|
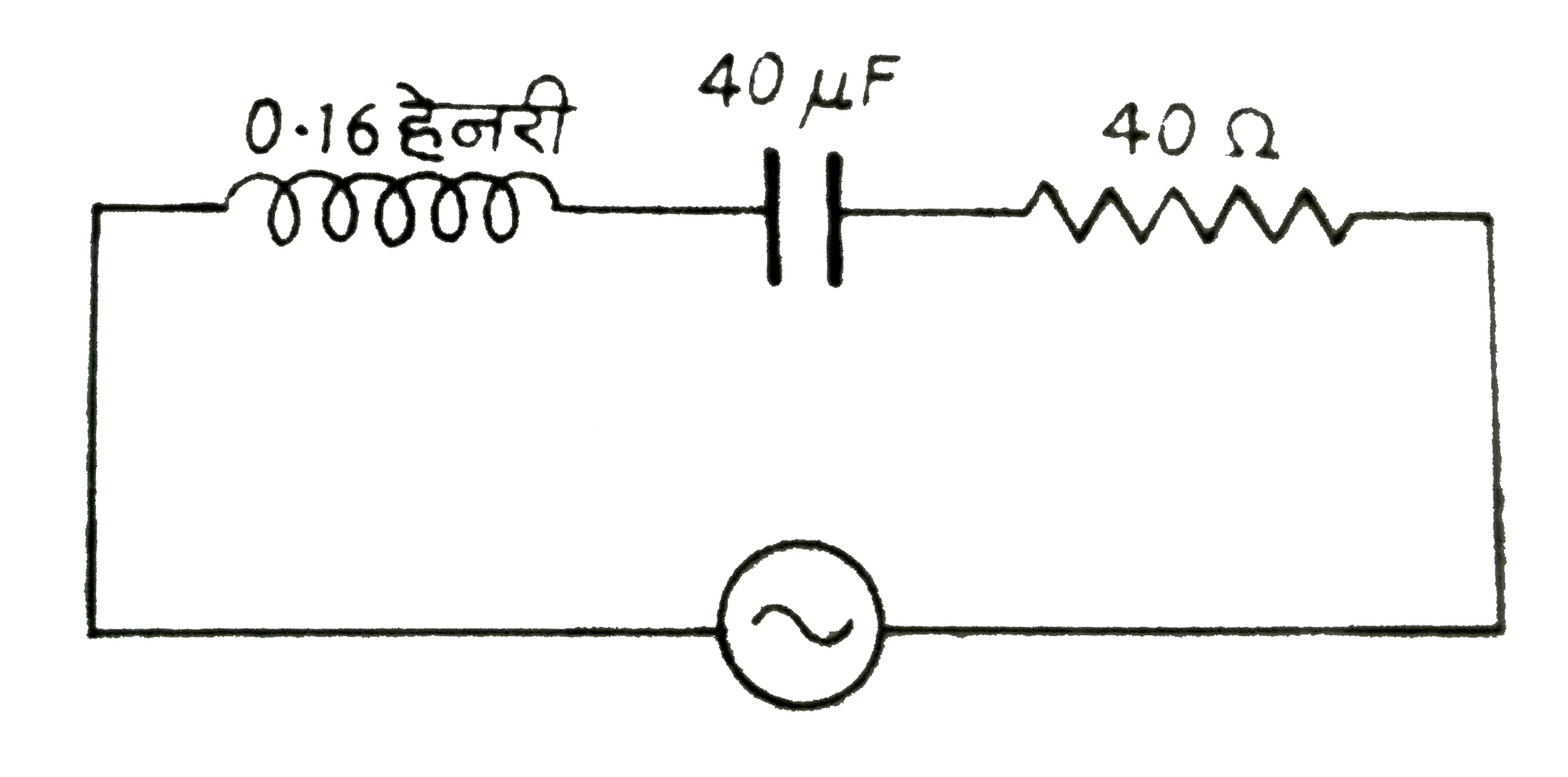
View Solutionचित्र में दिये गये परिपथ के लिये : (i) प्रतिबाधा, (ii) शक्ति गुणांक तथा (iii) धारा एवं वोल्टता के बीच कलान्तर ज्ञात कीजिये |

View Solutionसंलग्न चित्र 7.60 में एक L-C-R परिपथ दिखाया गया है | यह एक प्रत्यावर्ती धारा स्त्रोत वोल्टता V = 100 sin 500t परिपथ से जुड़ा है | परिपथ के लिए गणना कीजिये-(i) प्रतिबाधा, (ii) शक्ति गुणांक तथा (iii) धारा का शिखर मान |
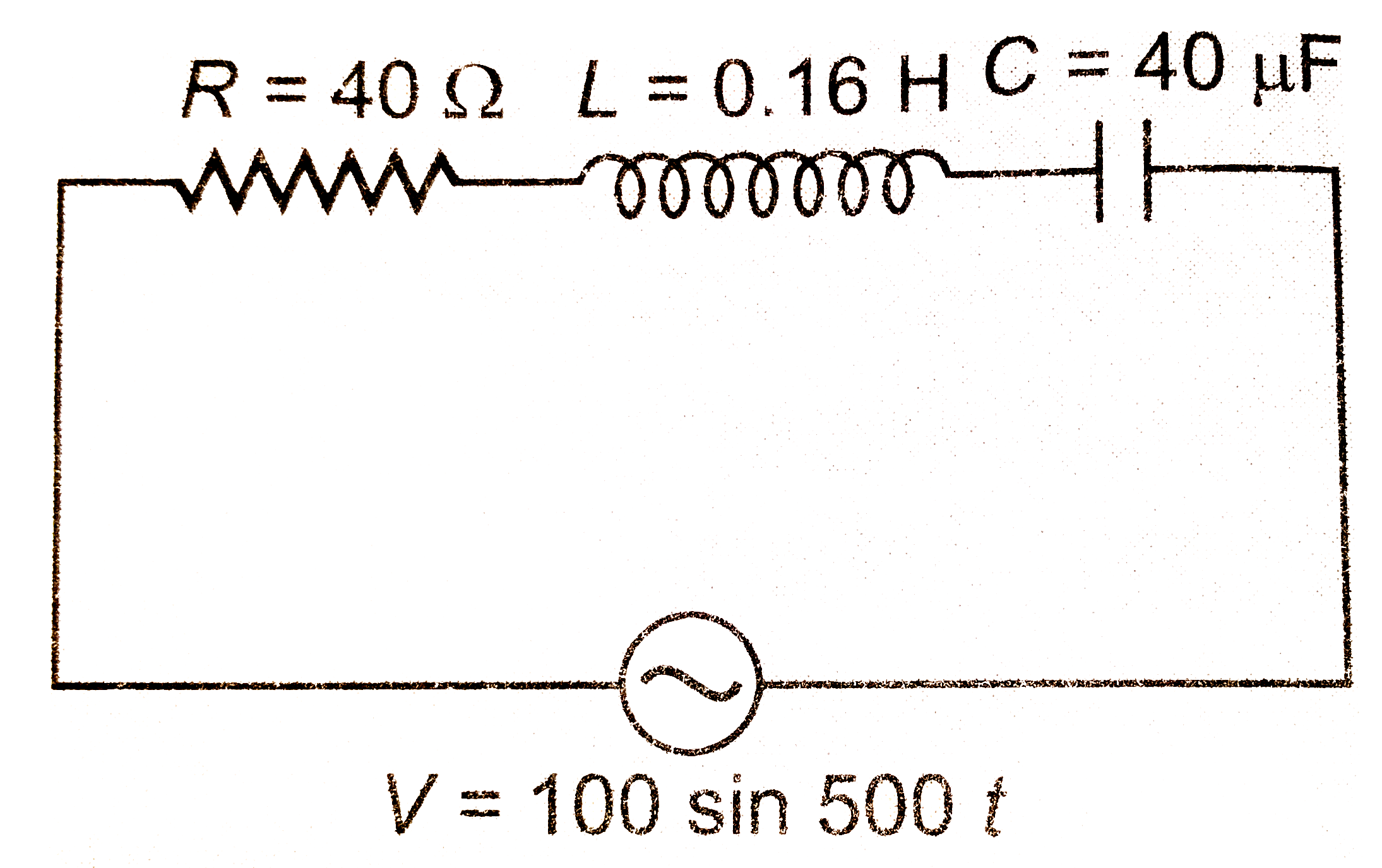
View SolutionL- C प्रत्यावर्ती परिपथ के लिए ज्ञात कीजिए-
(i) धारा एवं विभवान्तर में कलान्तर, (ii ) परिणामी विभवान्तर, (iii) परिपथ की प्रतिबाधा, (iv) अनुनाद की आवृत्ति, (v) इस परिपथ में धारा अधिकतम कब होती है ?
View Solutionकिसी प्रत्यावर्ती परिपथ में धारा ऐम्पियर तथा विभव वोल्ट है | परिपथ में शक्ति हानि है
View SolutionA circuit contains R, L and C connected in series with an A. C. source. The values of the reactances for inductor and capacitor are and respectively and the impedance of the circuit is Z1 . What happens to the impedance of the same circuit if the values of the reactances are interchanged:-
View Solutionनिम्नांकित चित्र में प्रदर्शित परिपथ के लिये :
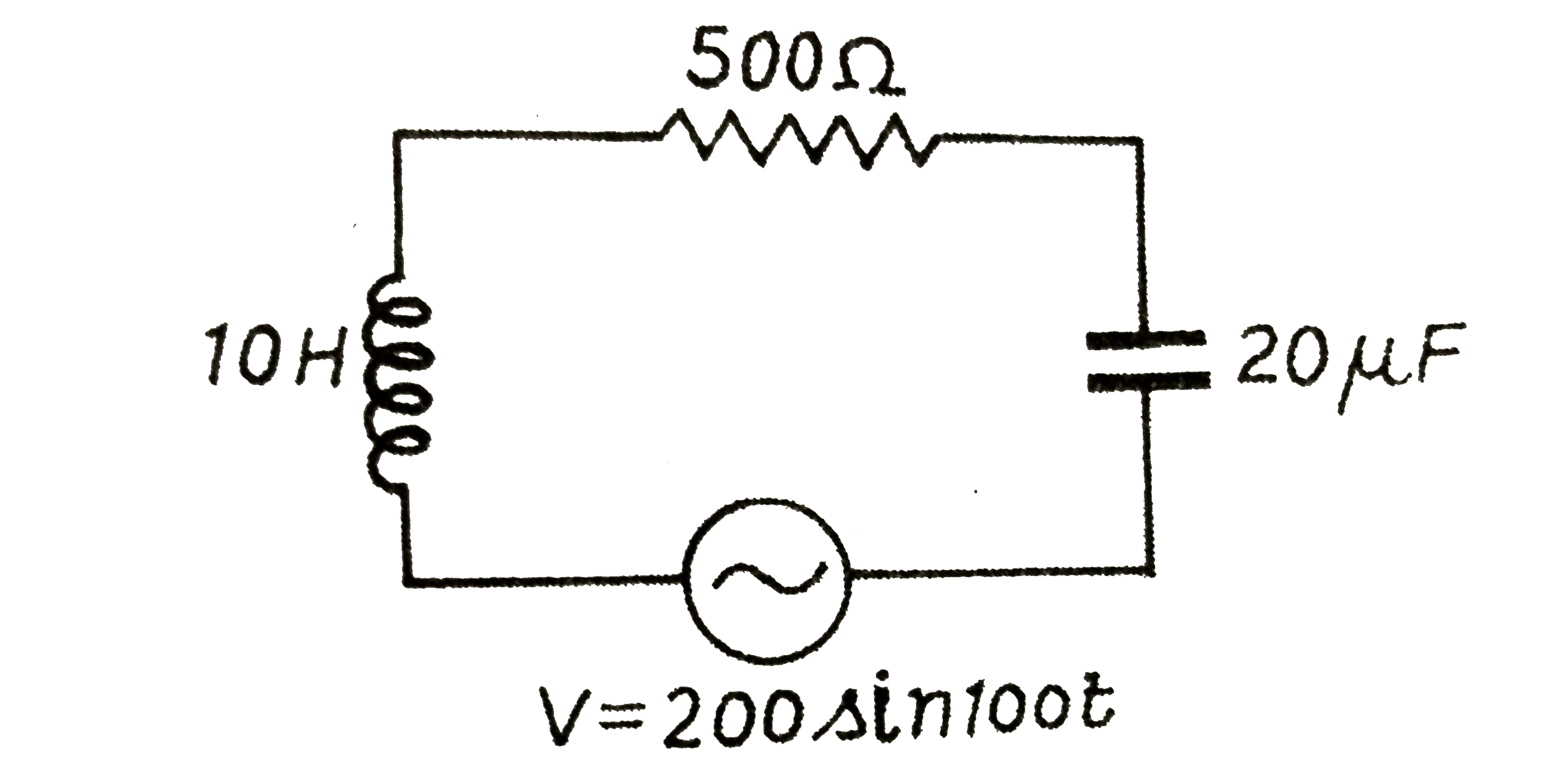
(i) प्रतिबाधा (ii) शक्ति - गुणाक तथा (iii) धारा एव वोल्टता के बीच कलान्तर ज्ञात कीजिए ।
View Solutionसलग्न चित्र में प्रदर्शित परिपथ के लिए ज्ञात कीजिए -
(i) प्रतिबाधा ,
(ii) शक्ति गुणांक ,तथा
(iii) धारा एवं वोल्टता के बीच कलांतर ।
View SolutionA capacitor and a resistor are connected in series with an a.c. source. If the potential difference across C, R are 120 V, 90 V, respectively and if the rms current of the circuit is 3 A, calculate the (i) impedance, (ii) power factor of the circuit.
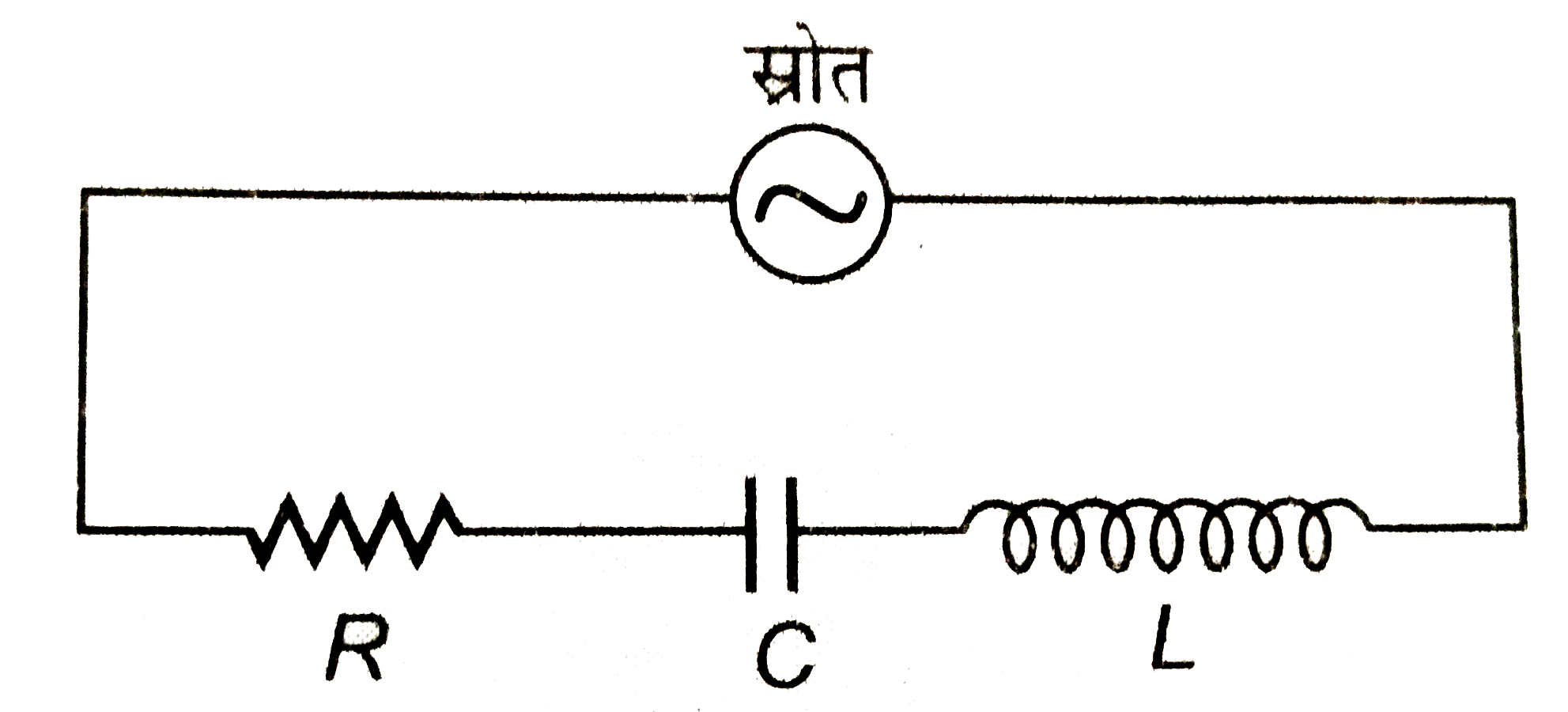
View Solutionएक स्त्रोत के वि० वा० बल की समीकरण है | स्त्रोत का आन्तरिक प्रतिरोध 1000 ओम है | एक परिपथ में प्रेरकत्व धारिता तथा प्रतिरोध ओम चित्र 7.52 की भाँति जोड़ा गया है | ज्ञात कीजिये- (i) वोल्टेज का शिखर मान, (ii) स्त्रोत की आवृत्ति,(iii) प्रेरण प्रतिघात (iv) धारितीय प्रतिघात, (v) परिपथ में प्रतिबाधा, (vi) शक्ति गुणांक |
View Solutionएक प्रत्यावर्ती धारा परिपथ में प्रेरकत्व, संधारित्र एवं प्रतिरोध श्रेणीक्रम में जोड़े गये है | परिपथ में वोल्टेज एवं धारा के समीकरण निम्न है-
वोल्ट
ऐम्पियर
ज्ञात कीजिये-
(i) प्रत्यावर्ती धारा स्त्रोत की आवृत्ति
(ii) V तथा i के मध्य कलान्तर
(iii) परिपथ की प्रतिबाधा
(iv) परिपथ में औसत शक्ति क्षय
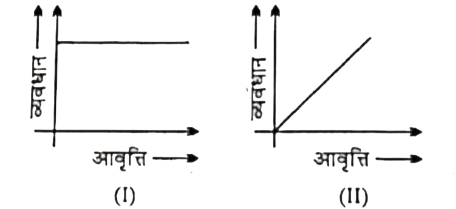
View Solution(i) ग्राफ (I) और (II) में आरोपित वोल्टता की आवृत्ति के साथ परिपथ अवयव के द्वारा प्रत्यावर्ती धारा के मार्ग में डाले गए व्यवधान (Opposition) को प्रदर्शित किया गया है। प्रत्येक ग्राफ के संगत परिपथ अवयव की पहचान कीजिए।
(ii) उपर्युक्त दोनों अवयवों के श्रेणी संयोजन द्वारा ac स्रोत से जोड़े जाने पर आरोपित प्रतिबाधा हेतु व्यंजक लिखिए। इस परिपथ में कौन-सा अग्रगामी होगा- वोल्टता या धारा?
View SolutionAn a.c. voltage V=Vm sin is applied across a
(i) series RC circuit in which the capacitive impedance is 'a' times the resistance in the circuit,
(ii) series RL circuit in which the inductive impedance is 'b' times the resistance in the circuit. Calculate the value of the power factor of the circuit in each case.
View Solutionप्रत्यावर्ती L-C-R परिपथ में ज्ञात कीजिए-
(i) परिणामी वोल्टेज, (ii) परिपथ की प्रतिबाधा, (iii) परिणामी वोल्टेज व धारा के मध्य कलान्तर।
View Solution