Find the forces in members BC BE FE of the truss shown in fig using method of section.
First find the support reaction which can be determined by considering equilibrium of the truss.∑V = 0 RA + RD = 50 ...iTaking moment about point A ∑MA = 0 – RD X 9 + 20 X 6 + 30 x 3 = 0 RD = 23.33KN ...iiNow from equation i; we getRA = 26.67KN ...iiiLet draw a section line 1-1 which cut the member BC BE FE and divides the truss in two parts RHS and LHS as shown in figa. Make the direction of forces only in those members which cut by the section line. Choose any one part of them Since both parts are separately in equilibrium. Let we choose right hand side portion as shown in figb. And the Right hand parts of truss is in equilibrium under the action of following forces 1. Reaction RD = 23.33KN2. 20KN load at joint C3. Force TBC in member BC From C to B 4. Force TBE in member BE From E to B5. Force TFE in member FE From E to FAll three forces are assumed to be tensileNow we take moment of all these five forces only from any point of the truss for getting the answers quicklyTaking moment about point E of all the five forces given above ∑ME = 0Moment of Force TBE TEF and 20KN about point E is zero since point E lies on the line of action of that forces– RD x ED + TEF x 0 + TBE x 0 – TBC x CE + 20 x 0 = 0– RD x 3 – TBC x 3 = 0TBC = – 23.33KN ... ivTBC = 23.33KN Compressive Taking moment about point B of all the five forces given above∑MB = 0Moment of Force TBE TBC force about point B is zero– RD x FD + TBC X 0 + TBE X 0 + TFE X CE + 20 X BC = 0– RD X FD + TFE X CE + 20 X BC = 0–23.33 X 6 + TFE X 3 + 20 X 3 = 0TFE = 26.66KN ...v TFE = 26.66KN Tensile Taking moment about point F of all the five forces given above∑MF = 0Moment of Force TFE about point B is zero– RD x FD – TBC x EC – TBE cos45º x FE + TFE x 0 + 20 x FE = 0–23.33 x 6 + 23.33 x 3 – TBE cos 45º x 3 + 20 x 3 = 0TBE = 4.71KNTBE = 4.71KN Tensile
Related Solutions
Find the resultant of the vectors shown in fig by the component method
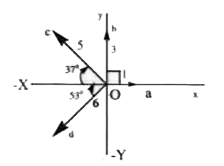
View SolutionFind the resultant of the vectors shown in fig by the component method.
View SolutionFind the resultant of the vectors shown in fig by the component method
View SolutionFind the resultant of the vectors shown in fig by the component method
View SolutionMethod 3 of W Mass of a piston shown in Fig. is m and area of cross-section is A. Initially spring is in its natural length. Find work done by the gas.
View SolutionMethod 3 of W Mass of a piston shown in Fig. is m and area of cross-section is A. Initially spring is in its natural length. Find work done by the gas.
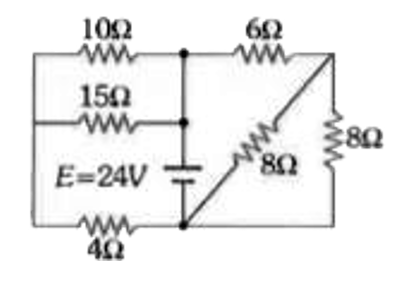
View Solutionचित्र में दिखाये गये परिपथ में, वि. वा. बल 24V के स्त्रोत के । परितः परिपथ का तुल्य प्रतिरोध ज्ञात करें
View SolutionFind the force of interaction between the bodies as shown in fig. Blocks are in contact.

View SolutionFind the force of interaction between the bodies as shown in fig. Blocks are in contact.

View SolutionThe net of the circuit displayed as shown in Fig. Find the force and the total internal resistance.
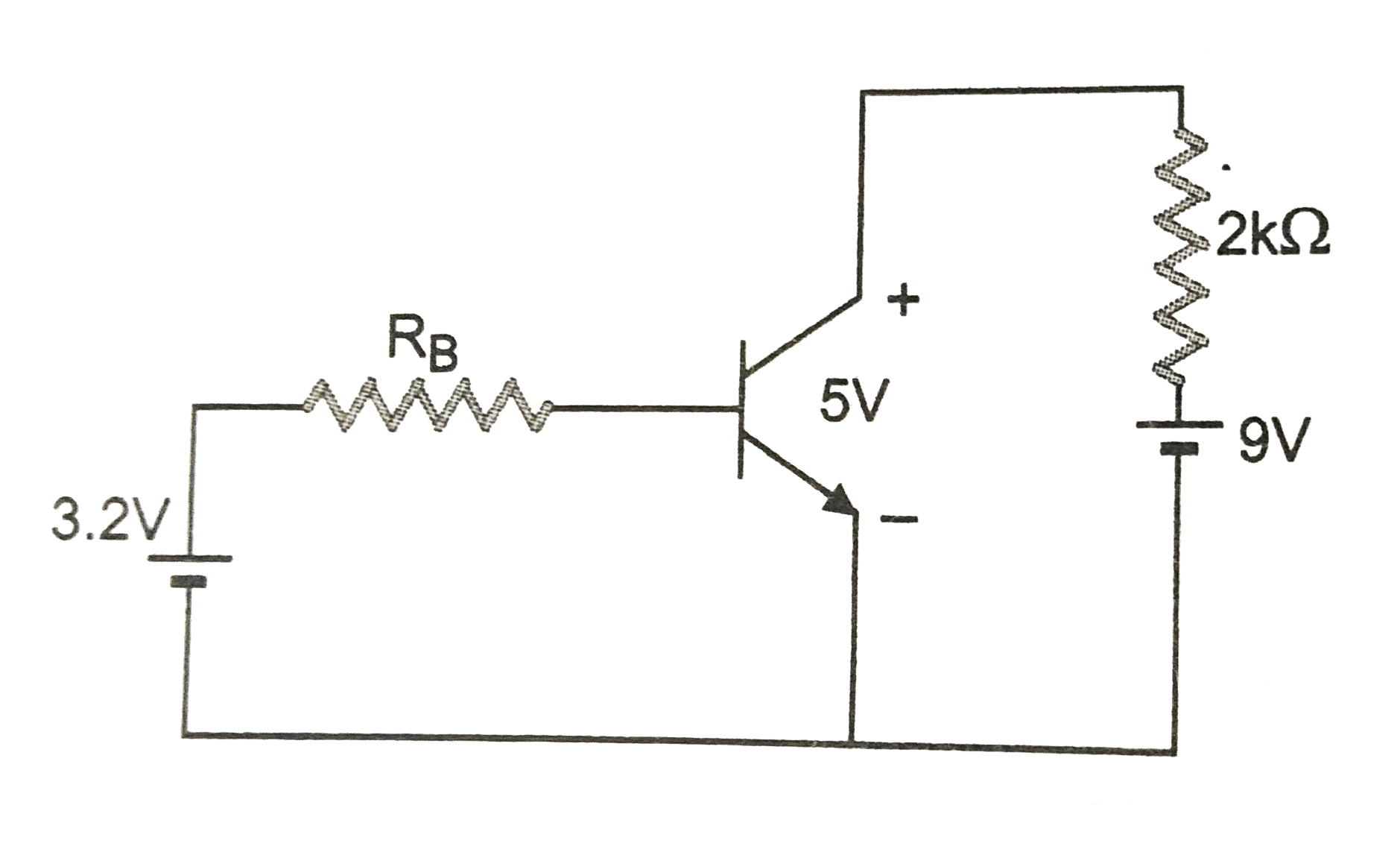
View SolutionIn which region transistor with operates as shown in Fig. Also find .
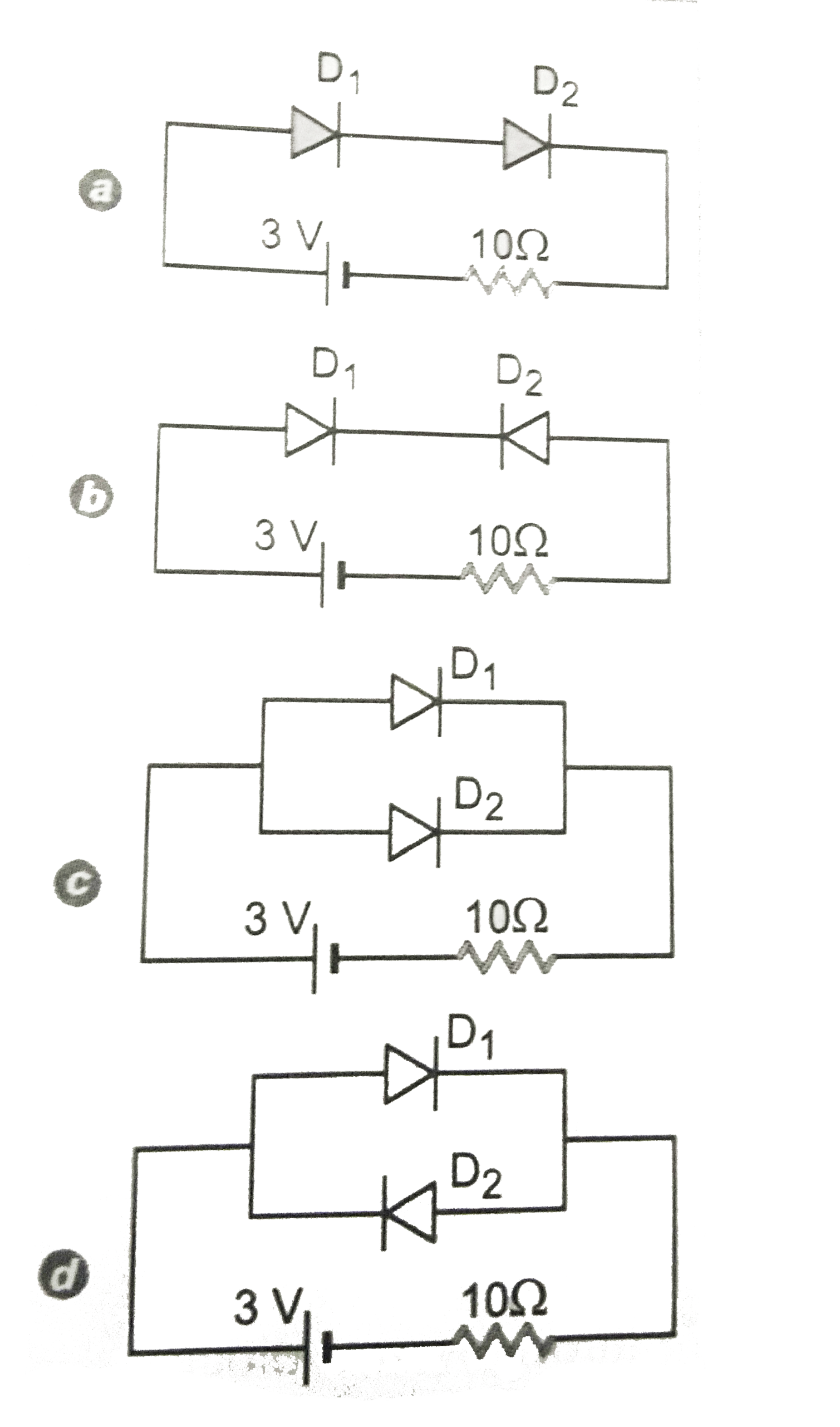
View SolutionFind the total current in the circuits shown in Fig. , , and . Each diode used is ideal
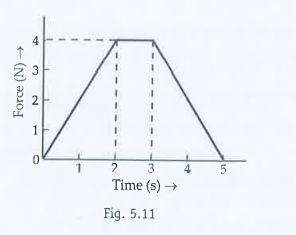
View SolutionA force acting on a body of mass 2 kg varies with time as shown in fig.5.11. Find impulse of the force.
View SolutionFind the magnetic field at the origin in the fig. Shown in fig.
View SolutionFind the magnetic field at the origin in the fig. Shown in fig.

View SolutionA weight of mass m hangs from a bracket (Fig.), AB = AC = BC = EC = a, DE = a/2. Find the forces in the rods.
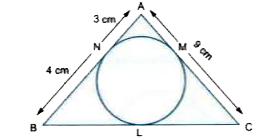
View SolutionIn Fig , is circumscribing a circle. Find the length of BC.
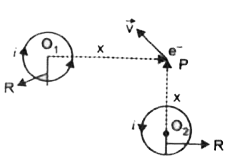
View SolutionThe magnetic force on an at point P as shown in fig . Is :
View SolutionDetermine the current in branches AB and BC of the network shown in Fig.
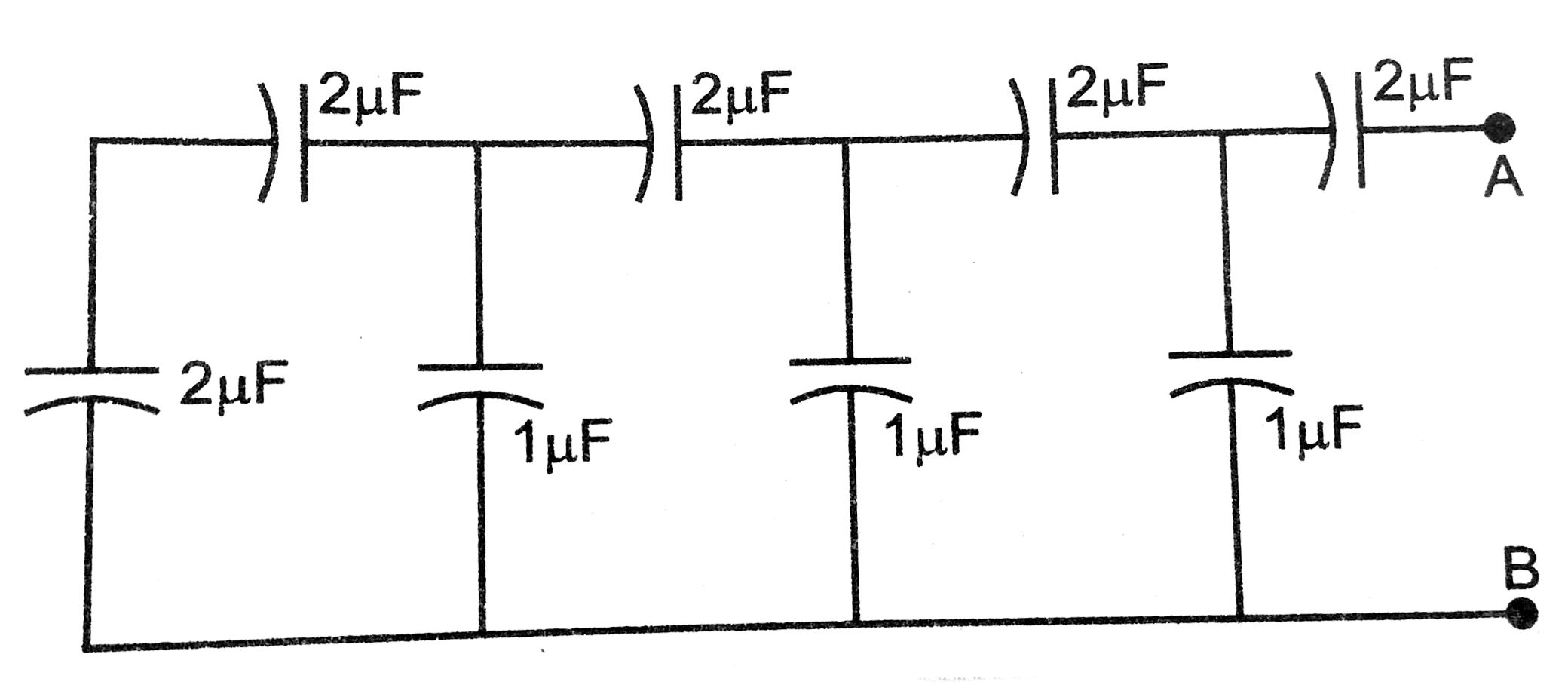
View SolutionFind the capacitance of the combination shown in Fig.
View Solution